Etiqueta: ejercicios resueltos python

Ejercicio: 1Eva_IT2005_T4 Lanza penales

Propuesta de solución en Python

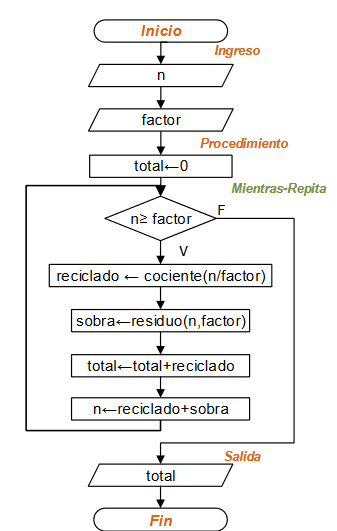
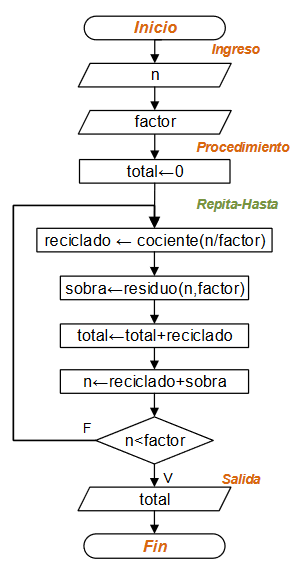
Se realiza el control de goles conseguidos en cada lanzamiento de balón, contando los lanzamientos hasta que se alcancen 5 .

El área dónde patea el balón el jugador se ingresa por teclado y la posición del arquero se obtiene de un aleatorio. Se analiza si hubo gol siempre que donde se patea sea diferente donde está el arquero, con lo que se contabiliza los goles conseguidos.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2005_T4 Lanza penales

import random as rnd

conseguido = 0
lanza = 0
while not(lanza==5):

    # Patea
    print('Penal número: ', lanza)
    patea = int(input('donde patea: '))
    while not(patea>=1 and patea<=6):
        patea = int(input('OE!..donde patea: '))

    # Arquero
    arquero = int(rnd.random() * 6) +1

    # Gol/tapa
    if not(patea==arquero):
        gol = 1
    else:
        gol = 0

    conseguido = conseguido + gol
    lanza = lanza + 1

    # Resultado
    print('patea, arquero, gol/tapa')
    print(patea, arquero, gol)

print('*** Goles conseguidos: ', conseguido)

Ejemplo de resultado del algoritmo:

Penal número:  0
donde patea: 3
patea, arquero, gol/tapa
3 3 0
Penal número:  1
donde patea: 2
patea, arquero, gol/tapa
2 6 1
Penal número:  2
donde patea: 1
patea, arquero, gol/tapa
1 1 0
Penal número:  3
donde patea: 2
patea, arquero, gol/tapa
2 4 1
Penal número:  4
donde patea: 3
patea, arquero, gol/tapa
3 5 1
*** Goles conseguidos:  3
>>>

Ejercicio: 1Eva_IT2005_T3 Arreglo aleatorio binario a decimal

Propuesta de solución en Python

Use un vector de n casillas, las casillas pueden iniciar en cero

B = np.zeros(n,dtype=int)

para luego llenarlas de números aleatorios una por una, mientras realiza las operaciones requeridas en el enunciado.

B[i] = int(rnd.random()*2)+0

De ser necesario repasar: Binario a Decimal – Algoritmo

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2005_T3 Arreglo aleatorio binario a decimal
# Tarea: contar los 1's, literal a)

import numpy as np
import random as rnd

# INGRESO
n = int(input('cuantos componentes n: '))

# PROCEDIMIENTO
B = np.zeros(n,dtype=int)
decimal = 0
i = 0
while (i<n):
    B[i] = int(rnd.random()*2)+0
    # orden de binarios es izquierda a derecha
    posicion = n-1-i  
    decimal  = decimal+B[i]*(2**posicion)
    i = i+1

# SALIDA
print('Arreglo de binarios B[i]:')
print(B)
print('equivale en decimal:',decimal)

Reaultados de algoritmo realizados para un byte (8 bits):

cuantos componentes n: 8
Arreglo de binarios B[i]:
[0 0 1 0 1 0 1 0]
equivale en decimal: 42
>>> 
cuantos componentes n: 8
Arreglo de binarios B[i]:
[1 1 1 1 1 1 1 1]
equivale en decimal: 255
>>> 
cuantos componentes n: 8
Arreglo de binarios B[i]:
[0 0 1 1 1 1 1 0]
equivale en decimal: 62
>>> 

Ejercicio: 2daEva_IIT2004_T3 Reciclar vasos

Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf

Se requiere usar el concepto de cociente y residuo, pues un vaso reciclado entero se obtiene con 4 vasos. Menos de 4 vasos a reciclar no producen un vaso entero, por lo que no se usan en el proceso y quedan separados como sobrantes a ser acumulados en el próximo ciclo.

Lazo mientras-repita

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IIT2004_T3 Reciclar vasos
# Solucion propuesta para 1ra Eval. sin Funciones

# INGRESO
n = int(input('Cuantos vasos usados:'))
factor = int(input('nuevos/reciclado:'))

# PROCEDIMIENTO
total=0
while (n>=factor):
    reciclado = n//factor
    sobra = n%factor
    total = total + reciclado
    n = reciclado + sobra

# SALIDA
print('total reciclados: ', total)

Lazo repita-hasta

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IIT2004_T3 Reciclar vasos
# Solucion propuesta para 1ra Eval. sin Funciones

# INGRESO
n = int(input('Cuantos vasos usados:'))
factor = int(input('nuevos/reciclado:'))

# PROCEDIMIENTO
total = 0
while not(n<factor):
    reciclado = n//factor
    sobra = n%factor
    total = total + reciclado
    n = reciclado + sobra

# SALIDA
print('total reciclados: ', total)

resultado del algoritmo

Cuantos vasos usados:70
nuevos/reciclado:4
total reciclados:  23
>>>
Cuantos vasos usados:7000
nuevos/reciclado:4
total reciclados:  2333
>>>

---

Diagrama de Flujo

Diagrama de Flujo con Repita-Hasta

ejercicios resueltos Python final_iit2004_t3 pdf

ejercicios resueltos Matlab final_iit2004_t3 pdf

Ejercicio: 2Eva_IIT2004_T1 Calcular raíz cúbica recursiva

# 2Eva_IIT2004_T1 Calcular raíz cúbica recursiva

def cubic(n, tolera = 0.0001):
    xi = 1
    diferencia = 1
    while (diferencia>tolera):
        xn = (2*(xi**3)+n)/(3*(xi**2))
        diferencia = abs(xn-xi)
        xi = xn
    return(xi)

resultado del algoritmo

>>> cubic(8)
2.0000000000120624
>>> cubic(27)
3.0000000000000973
>>> 

Ejercicio: 1Eva_IIT2004_T4 Matriz de paridad

Establecer una matriz de n filas y n+1 columnas. Para cada casilla en cada fila, columna, generar un aleatorio de dos posibilidades que mínimo puede ser cero, con lo que se genera la matriz de números aleatorios.

Al finalizar una fila, considere la suma de fila y revise el residuo de la división para 2.

Si hay residuo el número es impar y se debe escribir el número 1 en la última casilla de toda la fila (fila, n), es decir se completa la paridad.

En el caso opuesto, que no hay residuo, el conteo de ‘1’ ya es par y se deja el valor cero en la última casilla.

Instrucciones en Python

# 1Eva_IIT2004_T4 Matriz de paridad
import numpy as np
import random as rnd

# INGRESO
n = 7 # tamaño matriz

# PROCEDIMIENTO
# matriz de n filas y n+1 columnas
matriz = np.zeros(shape=(n,n+1),dtype=int)

# recorre matriz
for fila in range(0,n,1):
    sumafila = 0
    for columna in range(0,n,1):
        aleatorio = int(rnd.random()*2)+0
        matriz[fila,columna] = aleatorio
        sumafila = sumafila + aleatorio
    # revisa residuo paridad
    residuo = sumafila % 2  
    if residuo:
        matriz[fila,n] = 1

# SALIDA
print(' Matriz obtenida')
print(matriz)

resultado:

 Matriz obtenida
[[0 1 1 1 0 1 1 1]
 [1 1 0 1 0 0 1 0]
 [0 1 1 1 0 1 1 1]
 [1 0 0 1 1 0 1 0]
 [0 1 0 0 0 1 0 0]
 [1 0 0 0 1 1 0 1]
 [1 0 0 0 1 0 1 1]]
>>> 

Nota: Observe que la matriz contiene números aleatorios, por lo que el resultado varía cada vez que se ejecuta el algoritmo.

Ejercicio: 1Eva_IIT2004_T3 Estimar π por Montecarlo

Ingresar n como la cantidad de puntos en el plano a ubicar de forma aleatoria dentro del rango del cuadrado que inscribe al círculo. 

Usar una variable “k” como el contador para los puntos que caen dentro del círculo.

Al generar cada punto se puede calcular la distancia al centro mediante Pitágoras.

d= \sqrt{x^2 +y^2}

Se repite el proceso para n puntos y al final se calcula el valor estimado de pi acorde a la relación presentada.

Nota: no se usa como variable la palabra “pi” debido a que es nombre de variable reservada.

Instrucciones en Python

# 1Eva_IIT2004_T3 Estimar Pi por Montecarlo
# Propuesta de solución. edelros@espol.edu.ec
# se usa todo el círculo
import random as rnd
import numpy as np

# INGRESO
n = int(input('¿Cuántos puntos?: '))
radio = 1

# PROCEDIMIENTO
punto = np.zeros(shape=(n,2),dtype=float)
k = 0
i = 0
while i<n:
    x = rnd.random()*(2*radio)-1
    y = rnd.random()*(2*radio)-1

    d = np.sqrt(x**2+y**2)
    if d<=radio:
        k = k + 1
    punto[i] = [x,y]
    i = i + 1

estimadopi = 4*k/n

# SALIDA
print(k,n)
print('estimador pi: ', estimadopi)
print(punto)

la estimación de π con números aleatorios que se ubican dentro del círculo de radio 1 es:

¿Cuántos puntos?: 1000
781 1000
estimador pi:  3.124
[[ 0.15581724  0.43992571]
 [-0.11114653 -0.86426905]
 [ 0.51257751 -0.1969925 ]
 ...
 [ 0.26965478 -0.01555604]
 [-0.89575602  0.56077385]
 [ 0.33467618 -0.59497405]]
>>> 

---

Diagrama de Flujo

ejercicios resueltos Matlab parc_iit2004_t3 pdf

Ejercicio: 1Eva_IT2004_T3 Sortear parejas para tenis

Propuesta de solución en Python:

La variable n indica el número de parejas o tamaño de los vectores para almacenar la «pareja» y el contador de «veces» que juega cada una.

El ejercicio se divide en dos partes: la primera para seleccionar de forma aleatoria la pareja de la dama (una por una), es decir se sortean los caballeros (quien), y la segunda parte se realiza el proceso para los caballeros.

dama = n+1
while not(dama>(2*n)):
    quien = int(rnd.random()*n)+1
    pareja[dama] = quien
    veces[quien] = veces[quien]+1
    dama = dama + 1

En cada sorteo se registra cuántas veces participa cada uno.

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2004_T3 Sortear parejas para tenis

import random as rnd
import numpy as np

# INGRESO
n = int(input('cuantas parejas: '))

# PROCEDIMIENTO
pareja = np.zeros(2*n+1,dtype=int)
veces  = np.zeros(  n+1,dtype=int)

dama = n+1
while not(dama>(2*n)):
    quien = int(rnd.random()*n)+1
    pareja[dama] = quien
    veces[quien] = veces[quien]+1
    dama = dama + 1

# SALIDA
print(pareja[n+1:])
print('veces: ')
print(veces)

print('juegan varias veces: ')
caballero = 1
while not(caballero>n):
    if (veces[caballero]>1):
        print(caballero)
    caballero = caballero + 1

print('los que no juegan: ')
caballero = 1
while not(caballero>n):
    if (veces[caballero]==0):
        print(caballero)
    caballero = caballero + 1

con un ejemplo de resultado:

cuantas parejas: 10
[ 6  2  1  8  3  9 10  1  7  9]
veces: 
[0 2 1 1 0 0 1 1 1 2 1]
juegan varias veces: 
1
9
los que no juegan: 
4
5
>>> 

Ejercicio: 1Eva_IT2004_T2 Verificar ISBN

Propuesta de solución en Python

ISBN = 9684443242

Luego de pedir el número ISBN, se inicia extrayendo el dígito verificador escrito, quedando el resto de dígitos del número hacia la izquierda para realizar los cálculos.

vescrito = ISBN%10
n = ISBN//10

Tarea: verificar el número de dígitos del ISBN

Para la posición del dígito se usa un contador.

Las operaciones se acumulan en suma, de la que se obtiene el residuo de la división para 11.

El residuo corresponde al verificador calculado que se compara con el verificador escrito para dar el veredicto.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2004_T2 Verificar ISBN
# propuesta: edelros@espol.edu.ec

# INGRESO
ISBN = int(input('cual ISBN: '))

# PROCEDIMIENTO
vescrito = ISBN%10
n = ISBN//10

contador = 9
suma = 0
while (n>0):
    digito = n%10
    n = n//10
    suma =  suma + digito*contador
    contador = contador -1

vcalculado = suma%11

if (vescrito==vcalculado):
    respuesta = 1
else:
    respuesta = 0

#SALIDA
print(respuesta)

Resultado del algoritmo

cual ISBN: 9684443242
1
>>> 
cual ISBN: 9684443243
0
>>> 

Ejercicio: 2Eva_IIIT2003_T3 función distancia de Hamming

Se deben comparar las cadenas U y V en los elementos de las mismas posiciones.
Primero se plantea un algoritmo para determinar el número de parejas diferentes que existen dentro de cada cadena.

Si las cadenas difieren en el tamaño, la respuesta será ‘-1’.

Intrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IIIT2003_T3 Distancia de Hamming

# INGRESO
U = '20001'
V = '10103'

# PROCEDIMIENTO
n = len(U)
m = len(V)

diferente= -1  # tamaño diferente U,V
if n == m:
    diferente = 0
    i = 0
    while not(i>=n):
        if U[i] != V[i]:
            diferente = diferente +1
        i = i + 1
# SALIDA
print('distancia Hamming: ', diferente)

resultado del algoritmo

distancia Hamming:  3
>>> 

Luego se procede a convertir el algoritmo a una función y hacer la llamada desde un programa, con lo que se cumple lo requerido en cada literal

Instrucciones en Python usando una función

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IIIT2003_T3 Distancia de Hamming

# literal a. funcion
def dHamming(U,V):
    n = len(U)
    m = len(V)

    diferente = -1
    if n == m:
        diferente = 0
        i = 0
        while not(i>=n):
            if U[i] != V[i]:
                diferente = diferente +1
            i = i + 1
    return(diferente)

# Programa -------------
# INGRESO
U = '20001'
V = '10103'

# PROCEDIMIENTO
diferente = dHamming(U,V)

# SALIDA
print('distancia Hamming: ', diferente)

Tarea: Añadir la lectura de los datos desde un archivo.

Ejercicio: 2Eva_IIIT2003_T2 Raíz cuadrada por Newton

Recuerde que toda función recursiva requiere un valor inicial para la primera iteración. Empezando para n=0 con el valor de x:

f(1) = \frac{x}{2}

En el caso que n>1, se usa la expresión recursiva:

f(n) = 0.5\Bigg(f(n-1) + \frac{x}{f(n-1)}\Bigg)

Los valores tabulados para x=9 y n=10

ingrese x: 9
aproximación n-esima: 10
i , f(i)
0 nan
1 4.5
2 3.25
3 3.0096153846153846
4 3.000015360039322
5 3.0000000000393214
6 3.0
7 3.0
8 3.0
9 3.0
10 3.0
>>> 

Observe que a partir de la iteración 6, ya no muestra diferencia entre resultados consecutivos.

Para x= 9.5 con x=10

ingrese x: 9.5
aproximación n-esima: 10
i , f(i)
0 nan
1 4.75
2 3.375
3 3.0949074074074074
4 3.082233060472589
5 3.0822070015946474
6 3.0822070014844885
7 3.0822070014844885
8 3.0822070014844885
9 3.0822070014844885
10 3.0822070014844885
>>> 

---

Instrucciones en Python

La función no debe admitir valores de x negativos o cero, de darse el caso se responde np.NaN que corresponde a no es un número o ‘Not a Number’.

# 2Eva_IIIT2003_T2 Raíz cuadrada por Newton
import numpy as np

# literal a. función recursiva
def raizNewton(x,n)
    if n<=0 or x<=0:
        # no se admiten negativos o cero
        f = np.NaN
    else:
        if n == 1:
            f = x/2  # valor inicial
        if n>1:
            f = 0.5 *(raizNewton(x,n-1)+x/raizNewton(x,n-1))
    return (f)

# literal b. Programa ---------------
# INGRESO
x = float(input('ingrese x: '))
n = int(input('aproximación n-esima: '))

# PROCEDIMIENTO
print(' i , f(i)')
for i in range(0,n+1,1):
    print(i , raizNewton(x,i))