Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]
Referencia: Chapra 9.1 p247
Como punto de partida para la unidad de sistema de ecuaciones se usa un ejemplo para ilustrar con gráficos la solución para : 3 ecuaciones y 3 incógnitas.
La solución es un punto de intersección de los planos en el espacio dados por cada ecuación en el sistema.
La intersección entre dos planos es una recta, que al añadir un plano adicional la intersección es un punto. Las coordenadas del punto es la solución buscada.
Para generalizar y usar en otros casos, se realiza el desarrollo analítico del tema, junto al algoritmo y las gráficas en 3D en Python y Matplotlib.
Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]
..
1. Ejercicio
Referencia: 1Eva_IIT2011_T2 Sistema de Ecuaciones, diagonal dominante
Considere el siguiente sistema de ecuaciones:
\begin{cases} -2x+5y+9z=1\\7x+y+z=6\\-3x+7y-z=-26\end{cases}Se pueden representar como planos en el espacio despejando la variable z para cada ecuación, de la forma:
\begin{cases} z=(1+ 2x - 5y)/9\\z=(6 -7x-y)/1\\z=(-26+3x-7y)/(-1)\end{cases}Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]
..
2. Desarrollo analítico. Ecuaciones como Planos en el espacio
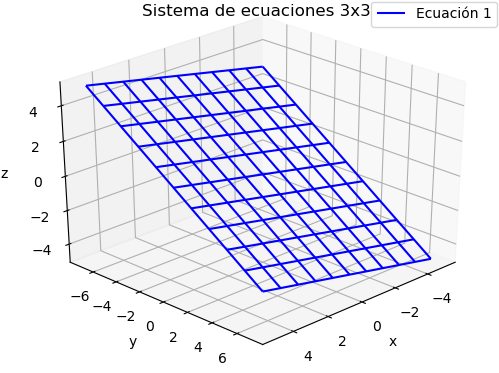
Si observamos la primera ecuación en una gráfica, encontramos que para graficar el plano se requiere definir los intervalos para los ejes X, Y, por ejemplo:
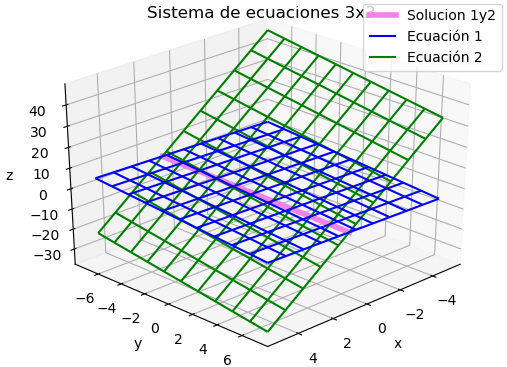
z=\frac{1+ 2x - 5y}{9} -5 \leq x \leq 5 -7 \leq y \leq 7
Al incorporar el plano de la segunda ecuación encontramos que la solución al sistema es la recta intersección de ambos planos.
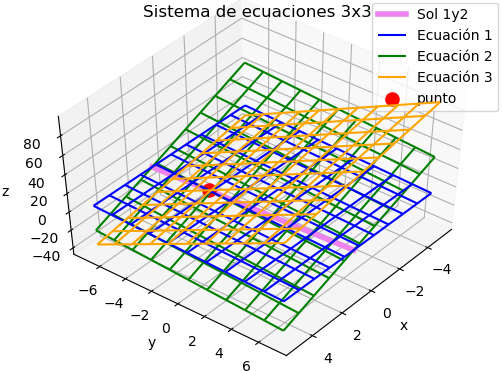
Usando la tercera ecuación, la intersección de los planos genera un punto cuyas coordenadas corresponden a la solución del sistema.
Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]
..
3. Algoritmo en Python
Para observar mejor del resultado en tres dimensiones, se plantean algunas instrucciones básicas para realizar la gráfica y obtener una mejor vista rotando el gráfico con el cursor.
Las ecuaciones del problema se pueden escribir en forma matricial Ax=B, usando solamente los coeficientes.
\begin{cases} -2x+5y+9z=1\\7x+y+z=6\\-3x+7y-z=-26\end{cases}# INGRESO Ax=B
A = np.array([[-2, 5, 9],
[ 7, 1, 1],
[-3, 7,-1]])
B = np.array([1,6,-26])
Con la forma matricial se generan las ecuaciones de cada plano usando los coeficientes al despejar la variable z.
Para visualizar los planos generados por cada ecuación se escribe cada ecuación como funciones(x,y) de dos variables. Para simplificar la escritura se usa el formato lambda.
# Ecuaciones de planos
z0 = lambda x,y: (-A[0,0]*x - A[0,1]*y + B[0])/A[0,2]
z1 = lambda x,y: (-A[1,0]*x - A[1,1]*y + B[1])/A[1,2]
z2 = lambda x,y: (-A[2,0]*x - A[2,1]*y + B[2])/A[2,2]
Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]
..
4. Gráficos. Intervalos de observación
Para la gráfica se requiere usar intervalos y muestras para las variables independientes x,y de forma semejante a las gráficas en 2D.
Las muestras en cada eje generan puntos en el plano X,Y y luego se usan todas las combinaciones que se generan.
– Primero se generan las muestras para cada eje en los vectores xi, yi.
ax = -5 # Intervalo [a,b] para eje x bx = 5 ay = ax-2 # Intervalo [a,b] para eje y by = bx+2 muestras = 11 xi = np.linspace(ax,bx, muestras) yi = np.linspace(ay,by, muestras)
con lo que se obtiene como resultado:
>>> xi array([-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.]) >>> yi array([-7. , -5.6, -4.2, -2.8, -1.4, 0. , 1.4, 2.8, 4.2, 5.6, 7. ]) >>>
– Las combinaciones entre las muestras de cada eje se obtienen generando las matrices Xi, Yi que representan la malla de muestras en el plano para evaluar cada punto.
Xi, Yi = np.meshgrid(xi,yi)
el resultado son las matrices con los puntos de evaluación en la malla. Por ejemplo el primer punto [x0,y0] = [-5,-7]:
>>> Xi array([[-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.], [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.]]) >>> Yi array([[-7. , -7. , -7. , -7. , -7. , -7. , -7. , -7. , -7. , -7. , -7. ], [-5.6, -5.6, -5.6, -5.6, -5.6, -5.6, -5.6, -5.6, -5.6, -5.6, -5.6], [-4.2, -4.2, -4.2, -4.2, -4.2, -4.2, -4.2, -4.2, -4.2, -4.2, -4.2], [-2.8, -2.8, -2.8, -2.8, -2.8, -2.8, -2.8, -2.8, -2.8, -2.8, -2.8], [-1.4, -1.4, -1.4, -1.4, -1.4, -1.4, -1.4, -1.4, -1.4, -1.4, -1.4], [ 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ], [ 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4, 1.4], [ 2.8, 2.8, 2.8, 2.8, 2.8, 2.8, 2.8, 2.8, 2.8, 2.8, 2.8], [ 4.2, 4.2, 4.2, 4.2, 4.2, 4.2, 4.2, 4.2, 4.2, 4.2, 4.2], [ 5.6, 5.6, 5.6, 5.6, 5.6, 5.6, 5.6, 5.6, 5.6, 5.6, 5.6], [ 7. , 7. , 7. , 7. , 7. , 7. , 7. , 7. , 7. , 7. , 7. ]]) >>>
– Se evalúan los puntos Xi,Yi en cada ecuación, que dan como resultado las matrices Zi
Z0 = z0(Xi,Yi) Z1 = z1(Xi,Yi) Z2 = z2(Xi,Yi)
Nota: Si es necesario, revise la sección de Gráficas 3D wireframe en la sección de Actividades y Recursos/Resumen Python.
El gráfico para cada ecuación ser realiza con la instrucción wireframe (malla de alambre) de las librerías 3D, se usa como entrada para el primer plano Xi,Yi,Z0. Luego se repite el procedimiento para Z1 y Z2.
Para simplicidad del algoritmo, pues la revisión del concepto es sobre intersección de planos, la solución se obtiene con las funciones de Numpy.
punto = np.linalg.solve(A,B)
El punto se incorpora a la gráfica como un punto usando scatter (dispersión).
Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]
..
5. Instrucciones en Python
# 1ra Evaluación II Término 2011 # Tema 2. Sistema de ecuaciones 3x3 # Concepto como interseccion de Planos import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import axes3d # INGRESO Ax=B A = np.array([[-2, 5, 9], [ 7, 1, 1], [-3, 7,-1]]) B = np.array([1,6,-26]) ax = -5 # Intervalo X bx = 5 ay = ax-2 # Intervalo Y by = bx+2 muestras = 11 # PROCEDIMIENTO -------- # Ecuaciones de planos z0 = lambda x,y: (-A[0,0]*x - A[0,1]*y + B[0])/A[0,2] z1 = lambda x,y: (-A[1,0]*x - A[1,1]*y + B[1])/A[1,2] z2 = lambda x,y: (-A[2,0]*x - A[2,1]*y + B[2])/A[2,2] xi = np.linspace(ax,bx, muestras) yi = np.linspace(ay,by, muestras) Xi, Yi = np.meshgrid(xi,yi) Z0 = z0(Xi,Yi) Z1 = z1(Xi,Yi) Z2 = z2(Xi,Yi) # solución al sistema punto = np.linalg.solve(A,B) # SALIDA print('respuesta de A.X=B : ') print(punto) # Interseccion entre ecuación 1 y 2 # PlanoXZ, extremo inferior de y Aa = np.copy(A[0:2,[0,2]]) Ba = np.copy(B[0:2]) Ba = Ba-ay*A[0:2,1] pta = np.linalg.solve(Aa,Ba) pa = np.array([ay]) pxza = np.array([pta[0],ay,pta[1]]) # PlanoXZ, extremo superior de y Ba = Ba-by*A[0:2,1] ptb = np.linalg.solve(Aa,Ba) pb = np.array([by]) pxzb = np.array([ptb[0],by,ptb[1]]) # GRAFICA de planos fig3D = plt.figure() graf3D = fig3D.add_subplot(111, projection='3d') graf3D.plot_wireframe(Xi,Yi,Z0, color ='blue', label='Ecuación 1') graf3D.plot_wireframe(Xi,Yi,Z1, color ='green', label='Ecuación 2') graf3D.plot_wireframe(Xi,Yi,Z2, color ='orange', label='Ecuación 3') # recta intersección planos 1 y 2 graf3D.plot([pxza[0],pxzb[0]], [pxza[1],pxzb[1]], [pxza[2],pxzb[2]], label='Sol 1y2', color = 'violet', linewidth = 4) # Punto solución del sistema 3x3 graf3D.scatter(punto[0],punto[1],punto[2], color = 'red', marker='o', label ='punto', linewidth = 6) graf3D.set_title('Sistema de ecuaciones 3x3') graf3D.set_xlabel('x') graf3D.set_ylabel('y') graf3D.set_zlabel('z') graf3D.set_xlim(ax, bx) graf3D.set_ylim(ay, by) graf3D.legend() graf3D.view_init(45, 45) # rotacion de ejes for angulo in range(45, 360+45, 5 ): graf3D.view_init(45, angulo) plt.draw() plt.pause(.001) plt.show()
Ejemplo: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Gráfico ] [ Python ]