Ejercicio: 1Eva_IT2010_T1_MN Demanda y producción sin,log
Desarrollo Analítico
Para la demanda, el intervalo de existencia es [0,3]
demanda(t) = sin(t)Para la oferta, el intervalo de existencia inicia en 1, limitado por la demanda [1,3]
oferta(t) = ln(t)la oferta satisface la demanda cuando ambas son iguales
demanda(t) = oferta(t) sin(t) = ln(t)por lo que el tiempo t se encuentra con algún método para determinar la raíz de:
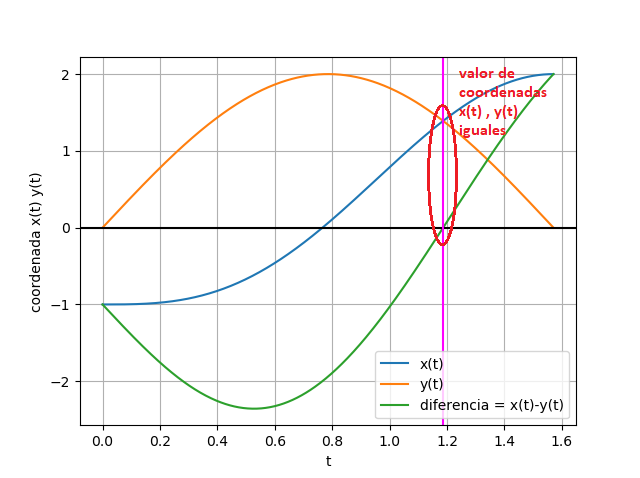
sin(t) - ln(t) = 0 f(t) = sin(t) - ln(t)Observe que las curvas de oferta y demanda se interceptan en el mismo punto en el eje x que la función f(t).
Para encontrar el valor de intersección de f(t) se propone usar el método de la bisección, en el intervalo [1,3]
itera = 0
a = 1, b =3
c=\frac{1+3}{2} = 2 f(1) = sin(1) - ln(1) = 0.8415 f(3) = sin(3) - ln(3) =-0.9575 f(2) = sin(2) - ln(2) =0.2162cambio de signo a la derecha
a =c = 2 , b = 3 tramo = |3-2| =1itera = 1
a = 2, b =3
c=\frac{2+3}{2} = 2.5 f(2) = 0.2162 f(3) =-0.9575 f(2.5) = sin(2.5) - ln(2.5) = -0.3178cambio de signo a la izquierda
a= 2 , b = c = 2.5 tramo = |2.5-2| = 0.5itera = 2
a = 2, b =2.5
c=\frac{2+2.5}{2} = 2.25 f(2) = 0.2162 f(2.5) = -0.3178 f(2.25) = sin(2.25) - ln(2.25) = -0.3178cambio de signo a la izquierda
a= 2 , b = c = 2.25 tramo = |2.25-2| = 0.25El resto de las iteraciones se continúan con el algoritmo,
encontrando la raíz en 2.219 usando tolerancia de 0.001
Algoritmo en Python
Desarrollo con el método de la Bisección usando el algoritmo:
método de Bisección i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)'] tramo 0 [1, 2.0, 3] [ 0.8415 -0.9575 0.2162] 1.0 1 [2.0, 2.5, 3] [ 0.2162 -0.9575 -0.3178] 0.5 2 [2.0, 2.25, 2.5] [ 0.2162 -0.3178 -0.0329] 0.25 3 [2.0, 2.125, 2.25] [ 0.2162 -0.0329 0.0965] 0.125 4 [2.125, 2.1875, 2.25] [ 0.0965 -0.0329 0.033 ] 0.0625 5 [2.1875, 2.21875, 2.25] [ 0.033 -0.0329 0.0004] 0.03125 6 [2.21875, 2.234375, 2.25] [ 0.0004 -0.0329 -0.0162] 0.015625 7 [2.21875, 2.2265625, 2.234375] [ 0.0004 -0.0162 -0.0079] 0.0078125 8 [2.21875, 2.22265625, 2.2265625] [ 0.0004 -0.0079 -0.0037] 0.00390625 9 [2.21875, 2.220703125, 2.22265625] [ 0.0004 -0.0037 -0.0017] 0.001953125 10 [2.21875, 2.2197265625, 2.220703125] [ 0.0004 -0.0017 -0.0007] 0.0009765625 raíz en: 2.2197265625
Instrucciones en Python
# 1Eva_IT2010_T1_MN Demanda y producción sin,log import numpy as np import matplotlib.pyplot as plt def biseccion(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=4): ''' Algoritmo de Bisección Los valores de [a,b] son seleccionados desde la gráfica de la función error = tolera ''' fa = fx(a) fb = fx(b) itera = 0 tramo = np.abs(b-a) if vertabla==True: print('método de Bisección') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') np.set_printoptions(precision) while (tramo>=tolera and itera<=iteramax): c = (a+b)/2 fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if vertabla==True: print(itera,[a,c,b],np.array([fa,fb,fc])) if (cambia<0): b = c fb = fc else: a = c fa = fc tramo = np.abs(b-a) if vertabla==True: print(' ',tramo) itera = itera + 1 respuesta = c # Valida respuesta if (itera>=iteramax): respuesta = np.nan return(respuesta) # INGRESO fx = lambda t: np.sin(t) - np.log(t) a = 1 b = 3 tolera = 0.001 # PROCEDIMIENTO respuesta = biseccion(fx,a,b,tolera,vertabla=True) # SALIDA print('raíz en: ', respuesta) # GRAFICA ad = 0 bd = 3 # intervalo oferta # considerando que no existe oferta negativa ao = 1 bo = 3 muestras = 21 demanda = lambda t: np.sin(t) oferta = lambda t: np.log(t) f = lambda t: demanda(t)-oferta(t) # PROCEDIMIENTO tid = np.linspace(ad,bd,muestras) demandai = demanda(tid) tio = np.linspace(ao,bo,muestras) ofertai = oferta(tio) fi = f(tio) # SALIDA plt.plot(tid,demandai, label='demanda') plt.plot(tio,ofertai, label ='oferta') plt.plot(tio,fi,label='f(t)= demanda-oferta') plt.axhline(0,color='black') plt.axvline(2.2185, color = 'magenta') plt.xlabel('tiempo') plt.ylabel('unidades') plt.legend() plt.grid() plt.show()