Ejercicio: 2Eva_2022PAOI_T3 EDP parabólica barra enfriada en centro
Para la ecuación dada con Δx = 1/3, Δt = 0.02, en una revisíón rápida para cumplir la convergencia dt<dx/10, condición que debe verificarse con la expresión obtenida para λ al desarrollar el ejercicio.
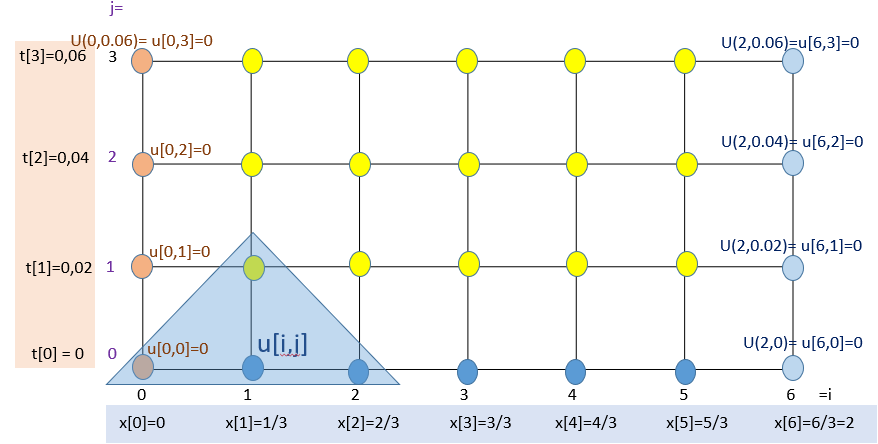
\frac{\partial U}{\partial t} - \frac{1}{9} \frac{\partial ^2 U}{\partial x^2} = 0 0 \leq x \leq 2, t>0literal a. grafica de malla
literal b. Ecuaciones de diferencias divididas a usar
\frac{\partial U}{\partial t} - \frac{1}{9} \frac{\partial ^2 U}{\partial x^2} = 0 \frac{\partial ^2 U}{\partial x^2} = 9 \frac{\partial U}{\partial t} \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = 9 \frac{u_{i,j+1}-u_{i,j}}{\Delta t}se agrupan las constantes,
\frac{\Delta t}{9(\Delta x)^2} \Big(u[i-1,j]-2u[i,j]+u[i+1,j] \Big) = u[i,j+1]-u[i,j]literal d Determine el valor de λ
\lambda = \frac{\Delta t}{9(\Delta x)^2} =\frac{0.02}{9(1/3)^2} = 0.02valor de λ que es menor que 1/2, por lo que el método converge.
continuando luego con la ecuación general,
\lambda \Big(u[i-1,j]-2u[i,j]+u[i+1,j] \Big) = u[i,j+1]-u[i,j] \lambda u[i-1,j]-2 \lambda u[i,j] + \lambda u[i+1,j] \Big) = u[i,j+1]-u[i,j]literal c. Encuentre las ecuaciones considerando las condiciones dadas en el problema.
\lambda u[i-1,j]+(1-2 \lambda ) u[i,j] + \lambda u[i+1,j] = u[i,j+1]el punto que no se conoce su valor es u[i,j+1] que es la ecuación buscada.
u[i,j+1] = \lambda u[i-1,j]+(1-2 \lambda ) u[i,j] + \lambda u[i+1,j]literal e iteraciones
iteración i=1, j=0
u[1,1] = \lambda u[0,0]+(1-2 \lambda ) u[1,0] + \lambda u[2,0] u[1,1] =0.02 \cos \Big( \frac{\pi}{2}(0-3)\Big) + (1-2(0.02) ) \cos \Big( \frac{\pi}{2}\big(\frac{1}{3}-3\big)\Big) + 0.02 \cos \Big( \frac{\pi}{2}\big( \frac{2}{3}-3\big) \Big) u[1,1] =0.02(0)+(0.96)(-0.5)+0.02(-0.8660)=-0.4973iteración i=2, j=0
u[2,1] = \lambda u[1,0]+(1-2 \lambda ) u[2,0] + \lambda u[3,0] u[2,1] = 0.02 \cos \Big( \frac{\pi}{2}(\frac{1}{3}-3)\Big) + (1-2(0.02) ) \cos \Big( \frac{\pi}{2}(\frac{2}{3}-3)\Big)+ + 0.02 \cos \Big( \frac{\pi}{2}\big(\frac{3}{3}-3\big)\Big) u[2,1] = 0.02 (-0.5) + (0.96 ) (-0.866025) + 0.02 (-1) =-0.8614iteración i=3, j=0
u[3,1] = \lambda u[2,0]+(1-2 \lambda ) u[3,0] + \lambda u[4,0] u[3,1] = 0.02 \cos \Big( \frac{\pi}{2}\big( \frac{2}{3}-3\big)\Big)+(1-2 (0.02) ) \cos \Big( \frac{\pi}{2}(1-3)\Big) + + 0.02 \cos \Big( \frac{\pi}{2}\big(\frac{4}{3}-3\big)\Big) u[3,1] = 0.02 (-0.866025)+(0.96 ) (-1) + 0.02 (-0,866025) = -0,9946literal f
la cotas de errores de truncamiento en la ecuación corresponden a segunda derivada O(hx2) y el de primera derivada O(ht), al reemplazar los valores será la suma}
O(hx2) + O(ht) = (1/3)2 + 0.02 = 0,1311
literal g
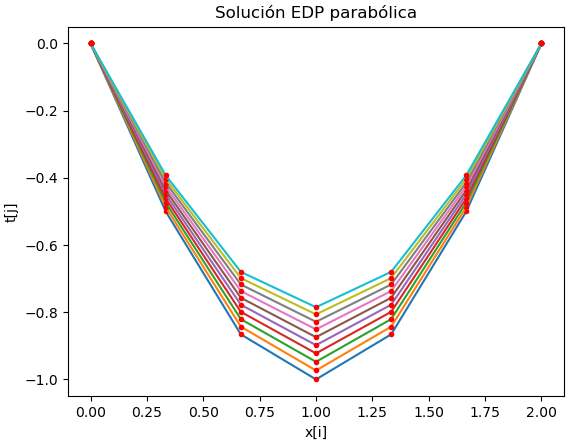
Resultados usando el algoritmo en Python
Tabla de resultados [[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [-0.5 -0.4973 -0.4947 -0.492 -0.4894 -0.4867 -0.4841 -0.4815 -0.479 -0.4764] [-0.866 -0.8614 -0.8568 -0.8522 -0.8476 -0.8431 -0.8385 -0.8341 -0.8296 -0.8251] [-1. -0.9946 -0.9893 -0.984 -0.9787 -0.9735 -0.9683 -0.9631 -0.9579 -0.9528] [-0.866 -0.8614 -0.8568 -0.8522 -0.8476 -0.8431 -0.8385 -0.8341 -0.8296 -0.8251] [-0.5 -0.4973 -0.4947 -0.492 -0.4894 -0.4867 -0.4841 -0.4815 -0.479 -0.4764] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]
Instrucciones en Python
# EDP parabólicas d2u/dx2 = K du/dt # método explícito, usando diferencias finitas # 2Eva_2022PAOI_T3 EDP parabólica barra enfriada en centro import numpy as np import matplotlib.pyplot as plt # INGRESO # Valores de frontera Ta = 0 Tb = 0 T0 = lambda x: np.cos((np.pi/2)*(x-3)) # longitud en x a = 0.0 b = 2.0 # Constante K K = 9 # Tamaño de paso dx = 1/3 dt = 0.02 tramos = int(np.round((b-a)/dx,0)) muestras = tramos + 1 # iteraciones en tiempo n = 10 # PROCEDIMIENTO # iteraciones en longitud xi = np.linspace(a,b,muestras) m = len(xi) ultimox = m-1 # Resultados en tabla u[x,t] u = np.zeros(shape=(m,n), dtype=float) # valores iniciales de u[:,j] j=0 ultimot = n-1 u[0,j]= Ta u[1:ultimox,j] = T0(xi[1:ultimox]) u[ultimox,j] = Tb # factores P,Q,R lamb = dt/(K*dx**2) P = lamb Q = 1 - 2*lamb R = lamb # Calcula U para cada tiempo + dt j = 0 while not(j>=ultimot): u[0,j+1] = Ta for i in range(1,ultimox,1): u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j] u[m-1,j+1] = Tb j=j+1 # SALIDA print('Tabla de resultados') np.set_printoptions(precision=2) print(u) # Gráfica salto = int(n/10) if (salto == 0): salto = 1 for j in range(0,n,salto): vector = u[:,j] plt.plot(xi,vector) plt.plot(xi,vector, '.r') plt.xlabel('x[i]') plt.ylabel('t[j]') plt.title('Solución EDP parabólica') plt.show()