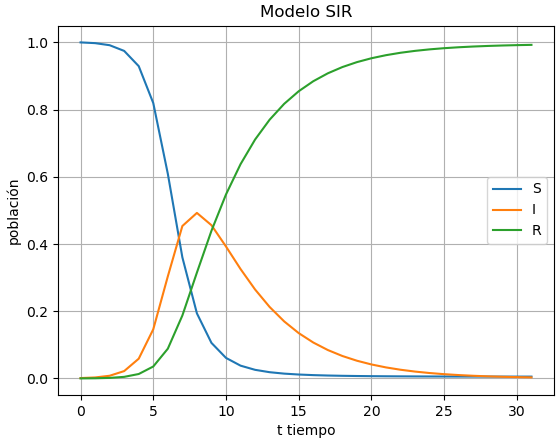
Ejercicio: 3Eva_2020PAOI_T2 Modelo epidemiológico no letal
El ejercicio representa un sistema de ecuaciones diferenciales ordinarias, que serán resueltas usando Runge-Kutta de 2do Orden.
De compararse con la curva de contagios de Covid-19 se tienen diferencias en la población recuperada, pues el modelo se considera no letal por lo que no se contabiliza el número de fallecidos.
El módelo es el más básico y permite cambiar por ejemplo la tasa de infección, y se ve los cambios en la curva de infectados. Se puede observar lo que se indicaba como objetivo de «aplanar la curva» al disminuir la población expuesta mediante cambiar la tasa de infección al exponer más o menos población al contagio por iteacción entre «suceptibles» e «infectados.
Desarrollo analítico
Las fórmulas para el algoritmo se identifican como:
binfecta = 1.4
grecupera = 1/4
que luego se usan en cada iteración que se registra en la tabla empezando con las condiciones iniciales
| itera | Si | Ii | Ri |
| 0 | 1 | 0.001 | 0 |
| 1 | 0.9977 | 0.002809 | 0.0003937 |
| 2 | 0.9916 | 0.007862 | 0.0014987 |
| 3 | tarea | … | … |
itera = 1
K_{1S} = h. f(t_i,S_i,I_i,R_i) =
itera = 2
K_{1S} = 1(-1.4)(0.9977)(0.002809) = -0.003924 K_{1I} = 1 \Big(1.4(0.9977)(0.002809) - \frac{1}{4}0.002809 \Big) = 0.003221 K_{1R} = 1(\frac{1}{4} 0.002809) = 0.0007022 K_{2S} = 1 \Big( -1.4*(0.9977-0.003924)(0.002809+0.003221) \Big) = = -0.008391 K_{2I} = 1 \Big(1.4(0.9977-0.003924)(0.002809+0.003221) - \frac{1}{4}(0.002809+0.003221) \Big) = 0.006883 K_{2R} = 1 \Big( \frac{1}{4}(0.002809+0.0032218) \Big) = 0.001507S_i = 0.9977 + \frac{-0.003924 -0.008391}{2} = 0.9916
I_i = 0.002809 + \frac{0.003221+0.006883}{2} = 0.007862
R_i = 0.0003937 + \frac{0.0007022 + 0.001507}{2} = 0.001498
t_i = t_i + h = 2 + 1 = 3
itera 3 – TAREA
Instrucciones en Python
# 3Eva_2020PAOI_T2 Modelo epidemiológico no letal # Sistemas EDO con Runge-Kutta de 2do Orden import numpy as np def rungekutta2_fgw(f,g,w,t0,x0,y0,z0,h,muestras): tamano = muestras +1 tabla = np.zeros(shape=(tamano,4),dtype=float) tabla[0] = [t0,x0,y0,z0] ti = t0 xi = x0 yi = y0 zi = z0 for i in range(1,tamano,1): K1x = h * f(ti,xi,yi,zi) K1y = h * g(ti,xi,yi,zi) K1z = h * w(ti,xi,yi,zi) K2x = h * f(ti+h, xi + K1x, yi+K1y, zi +K1z) K2y = h * g(ti+h, xi + K1x, yi+K1y, zi +K1z) K2z = h * w(ti+h, xi + K1x, yi+K1y, zi +K1z) xi = xi + (1/2)*(K1x+K2x) yi = yi + (1/2)*(K1y+K2y) zi = zi + (1/2)*(K1z+K2z) ti = ti + h tabla[i] = [ti,xi,yi,zi] tabla = np.array(tabla) return(tabla) # Programa # Parámetros de las ecuaciones binfecta = 1.4 grecupera = 1/4 # Ecuaciones f = lambda t,S,I,R : -binfecta*S*I g = lambda t,S,I,R : binfecta*S*I - grecupera*I w = lambda t,S,I,R : grecupera*I # Condiciones iniciales t0 = 0 S0 = 1.0 I0 = 0.001 R0 = 0.0 # parámetros del algoritmo h = 1.0 muestras = 51 # PROCEDIMIENTO tabla = rungekutta2_fgw(f,g,w,t0,S0,I0,R0,h,muestras) ti = tabla[:,0] Si = tabla[:,1] Ii = tabla[:,2] Ri = tabla[:,3] # SALIDA np.set_printoptions(precision=6) print(' [ ti, Si, Ii, Ri]') print(tabla) # Grafica tiempos vs población import matplotlib.pyplot as plt plt.plot(ti,Si, label='S') plt.plot(ti,Ii, label='I') plt.plot(ti,Ri, label='R') plt.title('Modelo SIR') plt.xlabel('t tiempo') plt.ylabel('población') plt.legend() plt.grid() plt.show()