Ejercicio: 3Eva_IT2009_T2 EDO Taylor Seno(x)
La ecuación del problema es:
xy'+ 2y = \sin (x) \frac{\pi}{2} \leq x \leq \frac{3\pi}{2} y\Big(\frac{\pi}{2} \Big) = 1Para el algoritmo se escribe separando y’:
y' = \frac{\sin (x)}{x} - 2\frac{y}{x}tomando como referencia Taylor de 3 términos más el término de error O(h3)
y_{i+1} = y_i +\frac{h}{1!}y'_i + \frac{h^2}{2!}y''_i + \frac{h^3}{3!}y'''_iSe usa hasta el tercer término para el algoritmo.
y_{i+1} = y_i +\frac{h}{1!}y'_i + \frac{h^2}{2!}y''_iSe determina que se requiere la segunda derivada para completar la aproximación. A partir de la ecuación del problema se aplica en cada término:
\Big(\frac{u}{v}\Big)' = \frac{u'v-uv' }{v^2} y'' = \frac{\cos (x) x - sin(x)}{x^2} - 2\frac{y'x-y}{x^2} y'' = \frac{\cos (x) x - sin(x)}{x^2} - 2\frac{\Big(\frac{\sin (x)}{x} - 2\frac{y}{x} \Big)x-y}{x^2}Con lo que se realizan las iteraciones para llenar la tabla
iteración 1
x0 = π/2= 1.57079633
y0= 1
y' = \frac{\sin (π/2)}{π/2} - 2\frac{1}{π/2} = -0.40793719 y'' = \frac{\cos (π/2) π/2 - sin(π/2)}{(π/2)^2}+ - 2\frac{(-0.40793719)(π/2)-1}{(π/2)^2}= 0.48531359 y_{1} = 1 +\frac{\pi/10}{1!}(-0.40793719) + \frac{(\pi/10)^2}{2!}(0.48531359) = 0.86x1 = x0+h = 1.57079633 + π/10 =1.88495559
iteración 2
x1 = 1.88495559
y1 = 0.86
y' = \frac{\sin (1.88495559)}{1.88495559} - 2\frac{0.86}{1.88495559} = -0.31947719 y'' = \frac{\cos (1.88495559)(1.88495559) - sin(1.88495559)}{(1.88495559)^2} - 2\frac{(-0.31947719) (1.88495559)-y}{(1.88495559)^2} = 0.16854341 y_{2} = 0.86 +\frac{\pi /10}{1!}(-0.31947719) + \frac{(\pi /10)^2}{2!}(0.16854341) = 0.75579202x2 = x1+ h = 1.88495559 + π/10 = 2.19911486
iteración 3
x2 = 2.19911486
y2 = 0.75579202
y' = \frac{\sin (2.19911486)}{2.19911486} - 2\frac{y}{2.19911486} = -0.29431724 y'' = \frac{\cos (2.19911486)(2.19911486) - sin(2.19911486)}{(2.19911486)^2} + - 2\frac{(-0.29431724)(2.19911486)-0.75579202}{(2.19911486)^2} = 0.0294177 y_{3} = 0.75579202 +\frac{\pi/10}{1!}(-0.29431724) + \frac{(\pi /10)^2}{2!}(0.0294177)x3 = x3+h = 2.19911486 + π/10 = 2.19911486
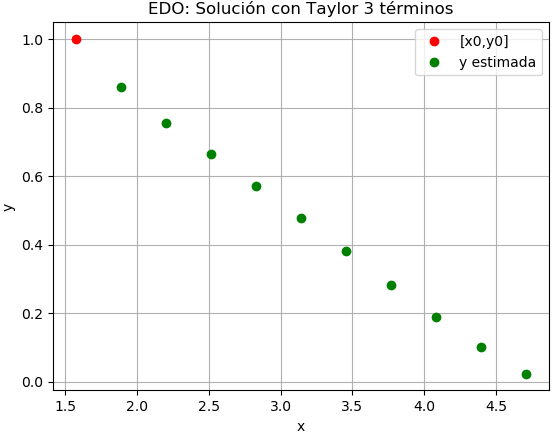
Con lo que se puede realizar el algoritmo, obteniendo la siguiente tabla:
estimado [xi, yi, d1y, d2y ] [[ 1.57079633 1. -0.40793719 0.48531359] [ 1.88495559 0.86 -0.31947719 0.16854341] [ 2.19911486 0.75579202 -0.29431724 0.0294177 ] [ 2.51327412 0.66374258 -0.29583247 -0.02247944] [ 2.82743339 0.5727318 -0.30473968 -0.02730493] [ 3.14159265 0.47868397 -0.31027009 -0.00585871] [ 3.45575192 0.38159973 -0.30649476 0.02930236] [ 3.76991118 0.28383639 -0.29064275 0.06957348] [ 4.08407045 0.18899424 -0.26221809 0.10859762] [ 4.39822972 0.10111944 -0.22243506 0.14160656] [ 4.71238898 0.02410027 0. 0. ]]
Algoritmo en Python
# 3Eva_IT2009_T2 EDO Taylor Seno(x) # EDO. Método de Taylor 3 términos # estima solucion para muestras separadas h en eje x # valores iniciales x0,y0 # entrega arreglo [[x,y]] import numpy as np def edo_taylor3t(d1y,d2y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,4),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0,0,0] x = x0 y = y0 for i in range(1,tamano,1): y = y + h*d1y(x,y) + ((h**2)/2)*d2y(x,y) x = x+h estimado[i-1,2:]= [d1y(x,y),d2y(x,y)] estimado[i,0:2] = [x,y] return(estimado) # PROGRAMA PRUEBA # 3Eva_IT2009_T2 EDO Taylor Seno(x). # INGRESO. # d1y = y', d2y = y'' d1y = lambda x,y: np.sin(x)/x - 2*y/x d2y = lambda x,y: (x*np.cos(x)-np.sin(x))/(x**2)-2*(x*(np.sin(x)/x - 2*y/x)-y)/(x**2) x0 = np.pi/2 y0 = 1 h = np.pi/10 muestras = 10 # PROCEDIMIENTO puntos = edo_taylor3t(d1y,d2y,x0,y0,h,muestras) xi = puntos[:,0] yi = puntos[:,1] # SALIDA print('estimado[xi, yi, d1yi, d2yi]') print(puntos) # Gráfica import matplotlib.pyplot as plt plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]') plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada') plt.title('EDO: Solución con Taylor 3 términos') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid() plt.show()