Ejercicio: 1Eva_2021PAOI_T2 Atención hospitalaria con medicamentos limitados
literal a
Se plantea el sistema de ecuaciones de acuerdo a la cantidad de medicamentos que se administra a cada tipo de paciente, siendo las variables X=[a,b,c,d] de acuerdo a la tabla:
| Niños | Adolescentes | Adultos | Adultos Mayores | Medicamentos /semana | |
| Medicamento_A | 0.3 | 0.4 | 1.1 | 4.7 | 3500 |
| Medicamento_B | 1 | 3.9 | 0.15 | 0.25 | 3450 |
| Medicamento_C | 0 | 2.1 | 5.6 | 1.0 | 6500 |
Mostrando que el número de incógnitas no es igual al número de ecuaciones, por lo que sería necesario de disponer de otra ecuación, o usar una variable libre.
literal b
Siguiendo las indicaciones sobre la variable libre que sea para el grupo de pacientes niños, te tiene que
0.4 b + 1.1 c + 4.7 d = 3500 - 0.3 K 3.9 b + 0.15 c + 0.25 d = 3450 - K 2.1 b + 5.6 c + 1.0 d = 6500 - 0 Ky haciendo K = 100, se convierte en :
0.4 b + 1.1 c + 4.7 d = 3500 - 0.3(100) = 3470 3.9 b + 0.15 c + 0.25 d = 3450 - 100 = 3350 2.1 b + 5.6 c + 1.0 d = 6500 - 0 = 6500literal c
Antes de desarrollar el ejercicio para el algoritmo se requiere convertir el sistema de ecuaciones a su forma matricial. Por lo que se plantea la matriz aumentada:
\begin{pmatrix} 0.4 & 1.1 & 4.7 & \Big| & 3470 \\ 3.9 & 0.15 &0.25 & \Big| & 3350 \\ 2.1 & 5.6 & 1.0 &\Big| & 6500\end{pmatrix}Se realiza el pivoteo parcial por filas, que al aplicar en la primera columa, se intercambia la primera y segunda fila, de tal forma que el mayor valor quede en la primera casilla de la diagonal.
\begin{pmatrix} 3.9 & 0.15 &0.25 & \Big| & 3350 \\ 0.4 & 1.1 & 4.7 & \Big| & 3470 \\ 2.1 & 5.6 & 1.0 &\Big| & 6500\end{pmatrix}se continua el mismo proceso para la segunda casilla de la diagonal hacia abajo, se aplica también pivoteo parcial,
\begin{pmatrix} 3.9 & 0.15 &0.25 & \Big| & 3350 \\ 2.1 & 5.6 & 1.0 &\Big| & 6500 \\ 0.4 & 1.1 & 4.7 & \Big| & 3470 \end{pmatrix}Con lo que el sistema queda listo para resolver por cualquier método.
Si seleccionamos Gauss-Seidel, el vector inicial de acuerdo al enunciado será X0=[100,100,100]
y las ecuaciones a resolver son:
b = \frac{3350 - 0.15 c - 0.25 d}{3.9} c = \frac{6500 - 2.1 b - 1.0 d}{5.6} d = \frac{3470- 0.4 b - 1.1 c}{4.7}iteración 1
X0=[100,100,100]
b = \frac{3350 - 0.15(100) - 0.25 (100)}{3.9} = 848.71 c = \frac{6500 - 2.1 (848.71 ) - 1.0 (100)}{5.6} = 824.58 d = \frac{3470- 0.4 (848.71 ) - 1.1 (824.58)}{4.7} = 473.07X1=[848.71, 824.58, 473.07]
diferencia = [848.71, 824.58, 473.07] – [100,100,100]
diferencia = [748.71, 724.58, 373.07]
error = max|diferencia| = 748.71
resultado del error es mayor que tolerancia de 0.01, se continua con la siguiente iteración.
iteración 2
X1=[848.71, 824.58, 473.07]
b = \frac{3350 - 0.15 (824.58) - 0.25 (473.07)}{3.9} = 796.93 c = \frac{6500 - 2.1 (796.93) - 1.0 (473.07)}{5.6} = 777.38 d = \frac{3470- 0.4 (796.93) - 1.1 (777.38)}{4.7} = 488.53X2 = [796.93, 777.38, 488.53]
diferencia = [796.93, 777.38, 488.53] – [848.71, 824.58, 473.07]
diferencia = [-51.78 , -47.2, 15.52]
error = max|diferencia| = 51.78
iteración 3
X2 = [796.93, 777.38, 488.53]
b = \frac{3350 - 0.15 (777.38) - 0.25 (488.53)}{3.9} = 797.75 c = \frac{6500 - 2.1 (797.75) - 1.0 (488.53)}{5.6} = 774.31 d = \frac{3470- 0.4 (797.75) - 1.1 (774.31)}{4.7} = 489.18x3 = [ 797.75, 774.31, 489.18]
diferencias = [ 797.75, 774.31, 489.18] – [796.93, 777.38, 488.53]
diferencias = [0.82, -3.07, 0.65]
error = max|diferencia| = 3.07
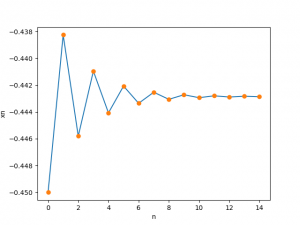
Observación, el error disminuye en cada iteración, por lo que el sistema converge.
solución con el algoritmo, solo se toma la parte entera de la respuesta, pues los pacientes son números enteros.
respuesta X: [797.83, 774.16, 489.20]
con lo que el primer resultado es:
X = [797, 774, 489]
literal d
Si la cantidad de pacientes presentados en una seman es la que se indica en el enunciado [350,1400,1500,1040], se determina que el sistema hospitalario estatal no podrá atender a todos los pacientes al compara con la capacidad encontrada en el literal c.
Hay un exceso de 2129 pacientes encontrados por grupo:
exceso = [350, 1400, 1500, 1040] – [100, 797, 774, 489] = [250, 603, 726, 551]
con lo que se recomienda una medida de confinamiento para disminuir los contagios y poder atender a los pacientes que se presenten.
literal e
Siendo K = 0, al estar vacunados todos los niños, y suponiendo que la vacuna es una cura, se tiene:
0.4 b + 1.1 c + 4.7 d = 3500 - 0.3 K = 3500 3.9 b + 0.15 c + 0.25 d = 3450 - K = 3450 2.1 b + 5.6 c + 1.0 d = 6500 - 0 k = 6500pivoteado parcialmente por filas se tiene:
\begin{pmatrix} 3.9 & 0.15 &0.25 & \Big| & 3450 \\ 2.1 & 5.6 & 1.0 &\Big| & 6500 \\ 0.4 & 1.1 & 4.7 & \Big| & 3500 \end{pmatrix}Resolviendo por un método directo:
se obtiene:
respuesta X: [823.46, 763.35, 495.94]
que al compararse con la capacidad anterior en números enteros se encuentra una diferencia de un incremento de 21 pacientes neto ante la condición de usar todos los medicamentos disponibles.
diferencia = [823, 763, 495] – [797, 774, 489] = [26, -11, 6]
Instrucciones en Python
# Método de Gauss-Seidel # solución de sistemas de ecuaciones # por métodos iterativos import numpy as np # INGRESO A = np.array([[0.4, 1.10, 4.7 ], [3.9, 0.15, 0.25], [2.1, 5.60, 1.0 ]]) k = 100 B = np.array([3500.-0.3*k,3450-1*k,6500-0*k]) X0 = np.array([100.0,100,100]) tolera = 0.001 iteramax = 100 # PROCEDIMIENTO # Matriz aumentada Bcolumna = np.transpose([B]) AB = np.concatenate((A,Bcolumna),axis=1) AB0 = np.copy(AB) # Pivoteo parcial por filas tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no está en diagonal if (dondemax !=0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal A = np.copy(AB[:,:n]) B = np.copy(AB[:,n]) # Gauss-Seidel tamano = np.shape(A) n = tamano[0] m = tamano[1] # valores iniciales X = np.copy(X0) diferencia = np.ones(n, dtype=float) errado = 2*tolera itera = 0 while not(errado<=tolera or itera>iteramax): # por fila for i in range(0,n,1): # por columna suma = 0 for j in range(0,m,1): # excepto diagonal de A if (i!=j): suma = suma-A[i,j]*X[j] nuevo = (B[i]+suma)/A[i,i] diferencia[i] = np.abs(nuevo-X[i]) X[i] = nuevo print(X) errado = np.max(diferencia) itera = itera + 1 # Respuesta X en columna X = np.transpose([X]) # revisa si NO converge if (itera>iteramax): X=0 # revisa respuesta verifica = np.dot(A,X) # SALIDA print('respuesta X: ') print(X) print('verificar A.X=B: ') print(verifica)