Ejercicio: 3Eva_IT2018_T1 Intersección de dos círculos
Para la solución se presentan dos secciones:
1. Solución particular de intersección de círculos
2. Solución General de intersección de círculos
_
1. Solución Particular de intersección de círculos
La solución particular se enfoca en el enunciado del ejercicio presentado
Literal a
Se grafica las funciones usando Python, para encontrar el rango de búsqueda de raíces.
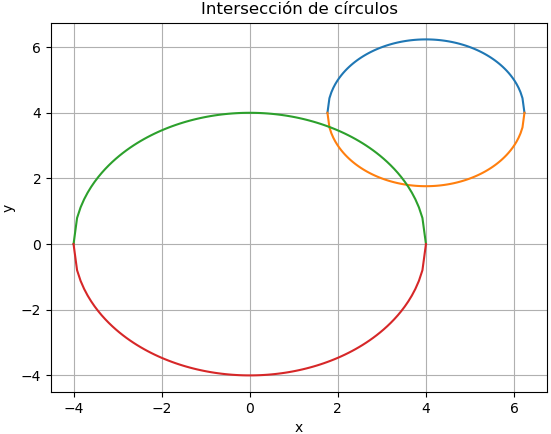
De la gráfica se usa el ‘zoom’ y se puede aproximar los valores para la intersección de las curvas estimando raices en x=1.80 y x=3.56
Desarrollo numérico
Se usan las ecuaciones para encontrar la diferencia entre las funciones.
(x-4)^2 + (y-4)^2 = 5
x^2 + y^2 = 16
Se despeja la variable y para la primera ecuación:
(y-4)^2 = 5 - (x-4)^2
y-4 = \sqrt{5 - (x-4)^2}
f(x) = y = \sqrt{5 - (x-4)^2} + 4
la segunda ecuacion se transforma en
x^2 + y^2 = 16
y^2 = 16 - x^2
g(x) = y = \sqrt{16 - x^2}
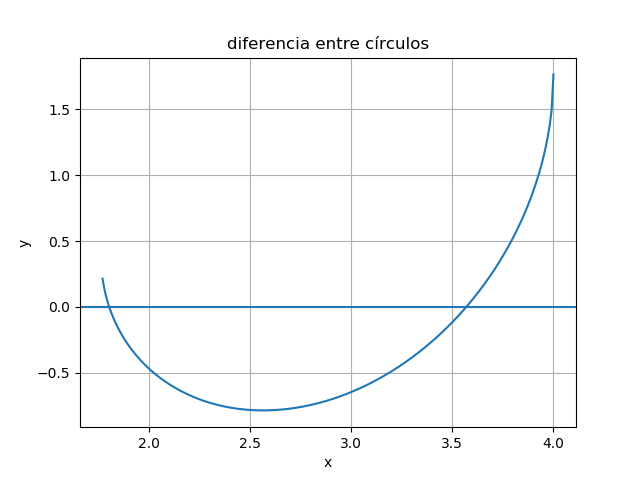
La intersección se obtiene restando las ecuaciones, para f(x) se usa la parte inferior del circulo y para g(x) la parte superior de circulo.
Para buscar las raices se analiza en el rango de existencia entre las dos funciones:
[-4,4]\text{ y } [4 -\sqrt{5} ,4 + \sqrt{5}]
[-4,4] \text{ y } [1.7639 , 6.2360]
por lo que la diferencia existe en el rango:
[1.7639 ,4]
\text{diferencia}(x) = f(x)-g(x)
que es el que se usa para el literal b
Literal b
Las ecuaciones para la diferencia entre las funciones son :
f_{2} (x) = -\sqrt{5-(x-4)^2}+4
g_{1} (x) = \sqrt{16-x^2}
Para el método de Newton-Raphson se requieren las derivadas:
\frac{d f_2}{dx} = \frac{x-4}{ \sqrt{5-(x-4)^2} }
\frac{d g_{1}}{dx} = \frac{-x}{ \sqrt{16-x^2} }
por lo que:
\frac{d \text{diferencia}}{dx} = \frac{d f_{2}}{dx} - \frac{d g_{1}}{dx}
Usando el algoritmo con Python se obtienen las raices:
usando Newton-Raphson
raices en: 1.80582463574 3.56917099898
Desarrollo en Python:
El desarrollo se realiza por partes, en el mismo orden del planteamiento de los literales
# 3ra Evaluación I Término 2018
# Tema 1. Intersección de círculos
import numpy as np
import matplotlib.pyplot as plt
# literal a
fx1 = lambda x: np.sqrt(5-(x-4)**2)+4
fx2 = lambda x: -np.sqrt(5-(x-4)**2)+4
gx1 = lambda x: np.sqrt(16-x**2)
gx2 = lambda x: -np.sqrt(16-x**2)
# Rango inicial de análisis (visual)
a = -5; b = 7
muestras = 501
# PROCEDIMIENTO
# Evalua los puntos en el rango
xi = np.linspace(a,b,muestras)
fx1i = fx1(xi)
fx2i = fx2(xi)
gx1i = gx1(xi)
gx2i = gx2(xi)
# SALIDA - Gráfica
plt.plot(xi,fx1i)
plt.plot(xi,fx2i)
plt.plot(xi,gx1i)
plt.plot(xi,gx2i)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Intersección de círculos')
plt.grid()
plt.show()
# GRAFICAR las diferencias
a = 4 - np.sqrt(5)
b = 4 + np.sqrt(5)
# PROCEDIMIENTO
xi = np.linspace(a,b,muestras)
diferencia = fx2(xi) - gx1(xi)
# GRAFICA
plt.plot(xi,diferencia)
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('y')
plt.title('diferencia entre círculos')
plt.grid()
plt.show()
# literal b -----------------------
def newton_raphson(funcionx, fxderiva, xi, tolera):
# funciónx y fxderiva en forma numérica
# xi es el punto inicial de búsqueda
tramo = abs(2*tolera)
while (tramo>=tolera):
xnuevo = xi - funcionx(xi)/fxderiva(xi)
tramo = abs(xnuevo-xi)
xi = xnuevo
return(xi)
funcionx = lambda x: fx2(x) - gx1(x)
fxderiva = lambda x: (x-4)/np.sqrt(5-(x-4)**2)+x/np.sqrt(16-x**2)
tolera = 0.001
xi1 = a + tolera
xi2 = 3.5
raiz1 = newton_raphson(funcionx, fxderiva, xi1, tolera)
raiz2 = newton_raphson(funcionx, fxderiva, xi2, tolera)
# SALIDA
print('\n usando Newton-Raphson')
print('raices en: ', raiz1,raiz2)
_
2. Solución General de intersección de círculos
Una solución más general de la intersección de círculos, considerada como para una actividad de mayor duración, revisa previamente si existe un cruce de áreas entre los dos círculos y estima el intervalo donde se encuentran las raíces [xa,xb].
De existir esa posibilidad, con el intervalo anterior [xa,xb] busca por un método de búsqueda de raíces las coordenadas de la intersección de las circunferencias.
2.1 Buscar cruce de áreas entre dos círculos
El cruce de áreas entre dos círculos se determina comparando si la distancia entre la suma de los radios es mayor o igual a la distancia entre los centros de los círculos.
De cumplirse la condicion anterior, es posible encontrar las intersecciones de los círculos. El valor xa se obtiene como el mayor entre los límites x hacia la izquierda de cada círculo, mientras que xb se obtiene como el límite x hacia la derecha entre los círculos.
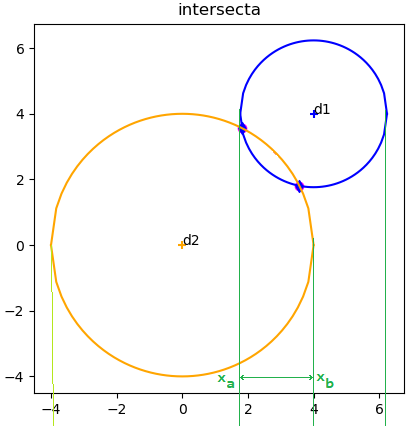
Lo siguiente que hay que reconocer es cuál de las partes (superior e inferior) de cada círculo es necesario usar para encontrar las intersecciones. Esta sección es necesaria puesto que la fórmula que describe el círculo contiene una raiz cuadrada que puede se positiva o negativa, generando dos segmentos en cada círculo.
Por ejemplo, partiendo de la fórmula general de un círculo con centro en [x1,y1] y radio r1:
(x-x_1)^2 + (y-y_1)^2 = r_1^2
(y-y_1)^2 = r_1^2 - (x-x_1)^2
\sqrt{(y-y_1)^2} = \sqrt{r_1^2 - (x-x_1)^2}
y = \sqrt{r_1^2 - (x-x_1)^2} + y_1
Con lo que se muestra la necesidad de ídentificar para cada círculo el sector arriba y abajo que interviene para encontrar las intersecciones. El orden del sector se establece con las posibles combinaciones de:
tabla de signos en raiz cuadrada para círculo
|
círculo 2 abajo |
círculo2 arriba |
| círculo 1 abajo |
[-1,-1] |
[-1,1] |
| círculo 1 arriba |
[ 1,-1] |
[ 1,1] |
El uso de cada combinación se estrablece en el vector de 1 y 0 con el siguiente orden:
sector = [ abajo1*abajo2, abajo1*arriba2,
arriba1*abajo2, arriba1*arriba2]
las instrucciones en Python para lo descrito se muestran como una función:
import numpy as np
import scipy.optimize as sp
def cruce2circulos(x1,y1,r1,x2,y2,r2):
''' Revisa intervalo de area de cruce
entre dos círculos de centro y radio
x1,y1,r1 // x2,y2,r2
'''
intersecta = []
dx = x2 - x1
dy = y2 - y1
d_centros = np.sqrt(dx**2 + dy**2)
d_cruce = r2 + r1
# los circulos se cruzan o tocan
if d_cruce >= d_centros:
# intervalos de cruce
xa = np.max([x1-r1,x2-r2])
xb = np.min([x1+r1,x2+r2])
ya = np.max([y1-r1,y2-r2])
yb = np.min([y1+r1,y2+r1])
# cada circulo arriba, abajo
abajo1 = 0 ; arriba1 = 0
abajo2 = 0 ; arriba2 = 0
if ya<=y1:
abajo1 = 1
if yb>=y1:
arriba1 = 1
if ya<=y2:
abajo2 = 1
if yb>=y2:
arriba2 = 1
sector = [ abajo1*abajo2, abajo1*arriba2,
arriba1*abajo2, arriba1*arriba2]
uncruce = [xa,xb,ya,yb,sector]
return(uncruce)
El resultado para los círculos del ejercicio son:
>>> x1=4; y1=4; r1=np.sqrt(5)
>>> x2=0; y2=0; r2=np.sqrt(16)
>>> uncruce = cruce2circulos(x1,y1,r1,x2,y2,r2)
>>> uncruce
[1.7639320225002102, 4.0,
1.7639320225002102, 2.23606797749979,
[0, 1, 0, 0]]
>>>
2.2 Raíces como coordenadas de intersección entre dos círculos
Las coordenadas de intersección entre dos círculos se obtienen aplicando un método de búsqueda de raíces. Por ejemplo bisección, que para esta parte se usa el algoritmo de SciPy con la instrucción sp.bisect(fx,xa,xb,xtol=2e-12).
Para el caso más general, donde existen dos raíces que buscar, se divide el intervalo de busqueda [xa,xb] en dos medios segmentos [xa,xc] y [xc,xb]. Se aplica un método de búsqueda de raíces para cada subintervalo. Para minimizar errores de truncamiento, en cada busqueda de desplaza dx/10 cada xc hacia el lado que amplia el subintervalo de búsqueda.
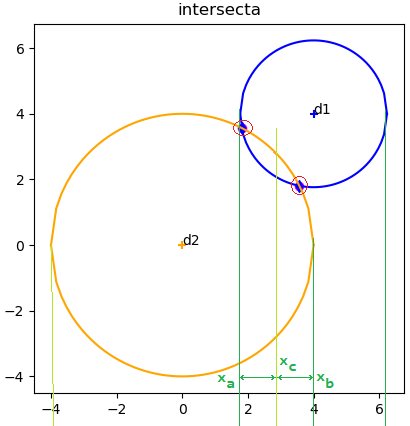
Para el caso donde los círculos solo tienen un punto de contacto, se realiza una revisión considerando que el intervalo de búsqueda podría ser menor al valor de tolerancia del radio.
Por ejemplo, cuando la linea que une los centros de los círculos resulta paralelos al eje de las x, adicionalmete se topan en un solo punto, el algoritmo anterior indica que se usan todos los sectores de los círculos, dando como resultado cuatro raices iguales. El caso se corrige realizando la parte de sectores solo cuando la distancia entre [xa,xb] es mayor a cero.
El resultado se presenta como los vectores raizx y raizy.
Las intrucciones en Python para esta sección se describen a continuación:
def raices2circulos(x1,y1,r1,x2,y2,r2,tolera=2e-12):
''' busca las intersección entre 2 circulos
de centro y radio: x1,y1,r1 || x2,y2,r2
revisa con cruce2circulos()
'''
uncruce = cruce2circulos(x1,y1,r1,x2,y2,r2)
raizx = []; raizy = []
# si hay cruce de circulos
if len(uncruce)>0:
sectores = [[-1,-1],[-1,1],
[ 1,-1],[ 1,1]]
[xa,xb,ya,yb,sector] = uncruce
xc = (xa+xb)/2
dx = np.abs(xb-xa)
dy = np.abs(yb-ya)
k = 1 # se tocan en un punto
if dx>0: # se tocan en mas de un punto
k = len(sector)
for j in range(0,k,1):
if sector[j]==1:
s1 = sectores[j][0]
s2 = sectores[j][1]
fx1 = lambda x: s1*np.sqrt(r1**2-(x-x1)**2)+y1
fx2 = lambda x: s2*np.sqrt(r2**2-(x-x2)**2)+y2
fx = lambda x: fx1(x)-fx2(x)
fa = fx(xa)
fb = fx(xb)
raiz1 = np.nan
raiz2 = np.nan
# intervalo/2 izquierda
xc = xc + dx/10
fc = fx(xc)
cambio = np.sign(fa)*np.sign(fc)
if cambio<0:
raiz1 = sp.bisect(fx,xa,xc,xtol=tolera)
# intervalo/2 derecha
xc = xc - 2*dx/10
fc = fx(xc)
cambio = np.sign(fc)*np.sign(fb)
if cambio<0:
raiz2 = sp.bisect(fx,xc,xb,xtol=tolera)
# si hay contacto en un borde
if dx<tolera*r1 and dy>0:
raiz1 = xa
if dy<tolera*r1 and dx>0:
raiz1 = x1
# Añade si existe raiz
if not(np.isnan(raiz1)):
raizx.append(raiz1)
raizy.append(fx1(raiz1))
if not(np.isnan(raiz2)):
raizx.append(raiz2)
raizy.append(fx1(raiz2))
raices = [raizx,raizy]
return(raices)
El resultado del algoritmo para el ejercicio es:
>>> raices = raices2circulos(x1,y1,r1,x2,y2,r2,tolera=2e-12)
>>> raices
[[1.805829001269906, 3.569170998730207],
[3.569170998734088, 1.8058290012706681]]
>>>