Ejercicio: 1Eva_IIT2018_T4 Tasa de interés en hipoteca
literal a
Siguiendo el desarrollo analítico tradicional, para adecuar la ecuación para los algoritmo de búsquda de raíces de ecuaciones, se reemplazan los valores en la fórmula.
P = A\Big(\frac{1-(1+i)^{-n}}{i} \Big) 70000 = 1200\Big(\frac{1-(1+i)^{-300}}{i} \Big)Como ambos lados de la ecuación deben ser iguales, si se restan ambos se obtiene una ecuación que tiene como resultado cero, que es la forma ideal para usar en el algoritmo que representa f(x) o en este caso f(i)
70000 - 1200\Big(\frac{1-(1+i)^{-300}}{i} \Big) = 0Para evitar inconvenientes con la división para cero en caso que i tome el valor de cero, dado se multiplica toda la ecuación por i:
i \Big[70000 - 1200\Big(\frac{1-(1+i)^{-300}}{i} \Big) \Big]= i (0) 70000 i - 1200 (1-(1+i)^{-300}) = 0La ecuación es la utilizada en el algoritmo de búsqueda de raíces pueden ser:
fx(i) = 70000 - 1200\Big(\frac{1-(1+i)^{-300}}{i} \Big) fx(i) = 70000i - 1200(1-(1+i)^{-300})literal b
El intervalo de existencia correspondería a la tasa de interés mínimo y el interés máximo.
[izquierda, derecha] = [a,b]
Para el intervalo se deben tomar en cuenta algunas consideraciones descritas a continuación:
izquierda:
En el extremo izquierdo, las tasas no son negativas, lo que se interpreta en que un banco paga por que le presten dinero.
Tampoco tiene mucho sentido el valor cero, que son prestamos sin intereses. A menos que sean sus padres quienes le dan el dinero.
Un valor inicial para el interés puede ser por ejemplo 1% ó 0.01, siempre que se cumpla que existe cambio de signo en la función a usar.
derecha:
En el extremo derecho, si se propone por ejemplo i con 100%, o 1.00, no tendría mucho sentido un préstamo con intereses al 100% anual, que resulta en el doble del valor inicial en tan solo un periodo o año.
La tasa de interés de consumo que son de las más alto valor, se encuentran reguladas. En Ecuador es un valor alrededor del 16% anuales o 0.16.
Considerando las observaciones iniciales del problema, se propone empezar el análisis para la búsqueda de la raíz en el intervalo en un rango más amplio:
[ 0.01, 0.50]
Ser realiza la comprobación que existe cambio de signo en los extremos del intervalo.
fx(0.001) =- 43935.86
fx(0.50) = 67600.0
Para el ejercicio se hace notar que la es tasa nominal anual, pero los pagos son mensuales. Por lo que se debe unificar las tasas de interes a mensuales. Una aproximación es usar las tasas anuales divididas para los 12 meses del año.
Tolerancia al error
La tolerancia se considera en éste ejercicio como el valor de diferencias (tramo) entre iteraciones con precisión satisfactoria.
Por ejemplo si no negociaremos más con el banco por variaciones de tasas del 0.1% , entonces la tolerancia será de 0.001.
Las publicaciones de tasas en el mercado incluyen dos decimales, por lo que para el ejercicio aumentamos la precisión a : 0.0001
tolera = 1×10-4
Literal c
Se presentan dos formas se solución para el litera c:
– c.1 la requerida en el enunciado con Newton-Raphson
– c.2 una alterna con el método de la Bisección.
c.1. Desarrollo del ejercicio con el método del enunciado Newton-Raphson
Para el método de Newton-Raphson se tiene que:
x_{i+1} = x_{i} - \frac{f(x_0i)}{f'(x_i)}Se requiere la derivada de la función planteada en el literal a:
fx(i) = 70000i - 1200(1-(1+i)^{-300}) f'x(i) = 70000 + 1200(300)(1+i)^{-301})tomando como valor inicial xi = 0.16/12 ≈ 0.013
Se realizan las iteraciones suponiendo que tolera = 1×10-4
iteración 1
fx(0.013) = 70000(0.013) - 1200(1-(1+0.013)^{-300})= -265.0914
f'x(0.013) = 70000 + 1200(300)(1+0.013)^{-301})= 62623.3454
x_{2} = 0.013 - \frac{-265.0914}{63318.8456} = 0.01723error = |0.013 – 0.01723| = 0.004229
iteración 2
fx(0.01723) = 70000i - 1200(1-(1+0.0.01723)^{-300})= 13.2356
f'x(0.01723) = 70000 + 1200(300)(1+0.01723)^{-301}= 67895.5656
x_{3} = 0.01723 - \frac{13.2356}{67895.5656} = 0.01703error = |0.01723 – 0.01703| = 0.0001999
cuyo valr de error está casi dentro del valor de tolerancia,
que permite tomar el último valor como respuesta de tasa mensual
raiz = tasa mensual = 0.01703
Convirtiendo a la tasa tasa anual que es la publicada por las instituciones financieras se tiene que:
tasa anual nominal = 0.01703*12 = 0.2043
Teniendo como resultado una tasa anual de 20.43%
Algoritmo en Python
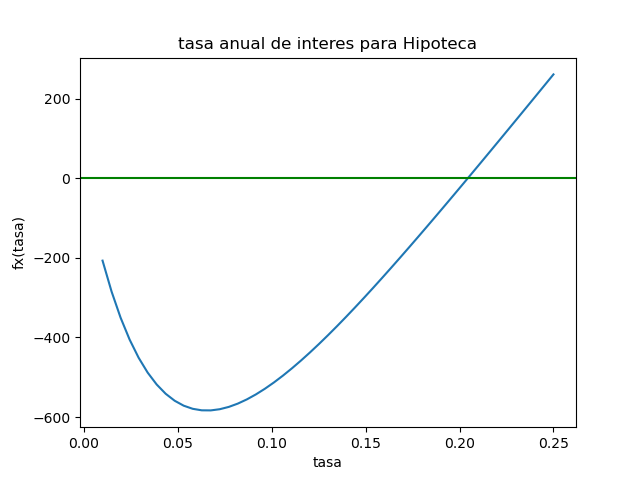
# 1ra Evaluación II Término 2018 # Tema 4. Tasa de interes para hipoteca import numpy as np import matplotlib.pyplot as plt def newton_raphson(fx, dfx, xi, tolera): ''' funciónx y fxderiva son de forma numérica xi es el punto inicial de búsqueda ''' tramo = abs(2*tolera) while (tramo>=tolera): xnuevo = xi - fx(xi)/dfx(xi) tramo = abs(xnuevo-xi) print(xi,xnuevo, tramo) xi = xnuevo return(xi) # INGRESO P = 70000.00 A = 1200.00 n = 25*12 fx = lambda i: P*i - A*(1-(1+i)**(-n)) dfx = lambda i: P + A*(-n)*(i+1)**(-n-1) a = 0.01/12 b = 0.25/12 muestras = 51 tolera = 0.0001 # PROCEDIMIENTO tasa = np.linspace(a,b,muestras) fi = fx(tasa) raiz = newton_raphson(fx, dfx, b, tolera) tanual = 12*raiz # SALIDA print('raiz encontrada en: ', raiz) print('tasa anual: ',tanual) # Gráfica plt.plot(tasa*12,fi) plt.title('tasa anual de interes para Hipoteca') plt.xlabel('tasa') plt.ylabel('fx(tasa)') plt.axhline(0, color='green') plt.show()
c.2. Desarrollo con el método de la Bisección
Desarrollo Analítico con Bisección
Como parte del desarrollo del ejercicio se presenta las iteraciones para el algoritmo, tradicionalmente realizadas con una calculadora.
fx(i) = 70000 - 1200\Big(\frac{1-(1+i)^{-300}}{i} \Big)iteración 1
a = 0.01, b = 0.5 c = \frac{a+b}{2} = \frac{0.01+0.5}{2} = 0.255 fx(0.01) = 70000 - 1200\Big(\frac{1-(1+(0.01))^{-300}}{0.01} \Big) = -43935.86 fx(0.255) = 70000 - 1200\Big(\frac{1-(1+(0.255))^{-300}}{0.255} \Big) = 65294.11 fx(0.5) = 70000 - 1200\Big(\frac{1-(1+(0.5))^{-300}}{0.5} \Big) = 67600.0 tramo = 0.5-0.01 =0.49cambio de signo a la izquierda
a = 0.01, b=0.255iteración 2
a = 0.01, b = 0.225 c = \frac{a+b}{2} = \frac{0.01+0.225}{2} = 0.1325 fx(0.01) = -43935.86 fx(0.1325) = 70000 - 1200\Big(\frac{1-(1+(0.1325))^{-300}}{0.1325} \Big) = 60943.39 fx(0.225) = 65294.11 tramo = 0.225-0.01 =0.215cambio de signo a la izquierda
a = 0.01, b=0.1325iteración 3
a = 0.01, b = 0.1325 c = \frac{a+b}{2} = \frac{0.01+0.1325}{2} = 0.07125 fx(0.01) = -43935.86 fx(0.07125) = 70000 - 1200\Big(\frac{1-(1+(0.07125))^{-300}}{0.07125} \Big) = 53157.89 fx(0.1325) = 60943.39 tramo = 0.1325-0.01 =0.1225cambio de signo a la izquierda
a = 0.01, b=0.07125y se continuaría con las iteraciones, hasta cumplir que tramo<=tolera
Tabla de datos obtenidos
| i | a | c | b | f(a) | f(c) | f(b) | tramo |
|---|---|---|---|---|---|---|---|
| 1 | 0.01 | 0.255 | 0.5 | -43935.86 | 65294.11 | 67600.0 | 0.49 |
| 2 | 0.01 | 0.1325 | 0.255 | -43935.86 | 60943.39 | 65294.11 | 0.215 |
| 3 | 0.01 | 0.07125 | 0.1325 | -43935.86 | 53157.89 | 60943.39 | 0.1225 |
hasta lo calculado la raiz se encontraría en el intervalo [0.01,0.07125] con error esitmado de 0.06125, aún por mejorar con más iteraciones.
Algoritmo en Python para Bisección
- El algoritmo bisección usa las variables a y b, por lo que los limites en el intervalo usados son [La,Lb]
- para el problema la variable ‘i’ se usa en el eje x.
- La selección de cambio de rango [a,b] se hace usando solo el signo del valor.
- El algoritmo presentado es tal como se explica en la parte conceptual
Se deja como tarea convertir el algoritmo a funcion def-return de Python.
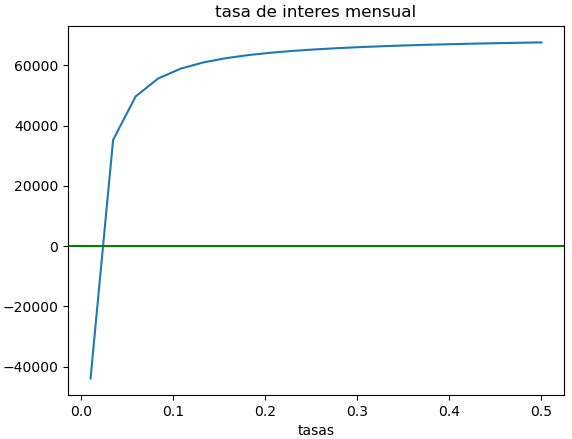
# 1Eva_IIT2018_T4 Tasa de interés en hipoteca import numpy as np import matplotlib.pyplot as plt # INGRESO P = 70000.00 A = 1200.00 n = 25*12 fi = lambda i: P - A*(1-((1+i)**-n))/i # Intervalo de observación # e inicio de Bisección La = 0.01 Lb = 0.50 tolera = 0.0001 #grafica muestras = 21 # PROCEDIMIENTO # Método de Bisección a = La b = Lb c = (a+b)/2 tramo = np.abs(b-a) while (tramo>tolera): fa = fi(a) fb = fi(b) fc = fi(c) cambio = np.sign(fc)*np.sign(fa) if (cambio>0): a = c b = b else: b = c a = a c = (a+b)/2 tramo = np.abs(b-a) # Para la gráfica tasa = np.linspace(La,Lb,muestras) fr = fi(tasa) # SALIDA print('a, f(a):', a,fa) print('c, f(c):', c,fc) print('b, f(b):', b,fb) print('la raiz esta entre: \n',a,b) print('con un error de: ', tramo) print('raiz es tasa buscada: ', c) print('tasas anual buscada: ',c*12) # Gráfica plt.plot(tasa,fr) plt.axhline(0, color='green') plt.title('tasa de interes mensual') plt.show()
la ejecución del algoritmo da como resultado
>>> RESTART: D:/MATG1052Ejemplos/HipotecaInteres.py a, f(a): 0.016998291015625 -385.52828922150366 c, f(c): 0.0170281982421875 -145.85350695741363 b, f(b): 0.01705810546875 92.28034212642524 la raiz esta entre: 0.016998291015625 0.01705810546875 con un error de: 5.981445312500111e-05 raiz es tasa buscada: 0.0170281982421875 tasas anual buscada: 0.20433837890625
y la gráfica obtenida es: