Categoría: Solución 3ra Evaluación

Ejercicio: 3Eva_IT2011_T2 producto de matrices

resultado obtenido:

producto es:
[[ 50.  50. 200. 450.]
 [ 75.  50.   0. 300.]
 [ 50. 100. 100. 150.]]
>>> 

Instrucciones en Python

# 3Eva_IT2011_T2 producto de matrices
import numpy as np

# INGRESO
A = [[2,1,2,3],
     [3,1,0,2],
     [2,2,1,1]]
B = [25,50,100,150]

# PROCEDIMIENTO
# usa arreglos en lugar de listas
A = np.array(A)
B = np.array(B)

tamano = np.shape(A)
n = tamano[0]
m = tamano[1]
k = len(B)

# verificar que m=k

C = np.zeros(shape=(n,m))
for i in range(0,n,1):
    for j in range(0,m,1):
        C[i,j] = A[i,j]*B[j]     

# SALIDA
print('producto es:')
print(C)

Ejercicio: 3Eva_IIT2011_T2 Registrar gastos en viaje por automóvil

Instrucciones en Python

# 3ra Evaluacion II Term 2011
# Tema 2. Recorridos Juan y Pedro
import random as rnd

# INGRESO
n = int(input('Ingrese cantidad de ciudades: '))
gasto = [0]
izquierda = [0]
derecha = [0]
for i in range(1,n+1,1):
    print("Ciudad: ", i)
    ungasto = int(input('Gastos en ciudad: '))
    ciudad_izq = int(input('Ciudad izquierda: '))
    ciudad_der = int(input('Ciudad  derecha: '))
    gasto.append(ungasto)
    izquierda.append(ciudad_izq)
    derecha.append(ciudad_der)

# PROCEDIMIENTO
# Viaje de Juan
dia    = 1
visita = 1
costojuan = 0
rutajuan  = []
while not(visita==0):
    rutajuan.append(visita)
    costojuan = costojuan + gasto[visita]
    direccion = int(rnd.random()*2)+1
    if direccion == 1:
        visita = izquierda[visita]
    else:
        visita = derecha[visita]
    dia = dia+1
diasjuan = dia-1


# Viaje de Pedro
dia    = 1
visita = 1
costopedro = 0
rutapedro  = []
while not(visita==0):
    rutapedro.append(visita)
    costopedro = costopedro + gasto[visita]
    direccion  = int(rnd.random()*2)+1
    if direccion == 1:
        visita = izquierda[visita]
    else:
        visita = derecha[visita]
    dia = dia+1
diaspedro = dia-1

# SALIDA
print('Recorrido de Juan: ', rutajuan)
print('Costo de Juan: ', costojuan)
print('Recorrido de Pedro: ', rutapedro)
print('Costo de Pedro: ', costopedro)

if diasjuan>diaspedro:
    print('Juan visitó más ciudades')
else:
    print('Pedro visitó más ciudades')

if costojuan<costopedro:
    print('Juan tuvo el viaje más barato')
else:
    print('Pedro tuvo el viaje más barato')

Resultado del algoritmo

RESTART: D:/CCPG1001Ejemplos/RutasJuanPedro.py 
Ingrese cantidad de ciudades: 7
Ciudad:  1
Gastos en ciudad: 200
Ciudad izquierda: 3
Ciudad  derecha: 2
Ciudad:  2
Gastos en ciudad: 150
Ciudad izquierda: 4
Ciudad  derecha: 5
Ciudad:  3
Gastos en ciudad: 70
Ciudad izquierda: 7
Ciudad  derecha: 4
Ciudad:  4
Gastos en ciudad: 140
Ciudad izquierda: 7
Ciudad  derecha: 6
Ciudad:  5
Gastos en ciudad: 90
Ciudad izquierda: 6
Ciudad  derecha: 0
Ciudad:  6
Gastos en ciudad: 300
Ciudad izquierda: 7
Ciudad  derecha: 0
Ciudad:  7
Gastos en ciudad: 50
Ciudad izquierda: 0
Ciudad  derecha: 0
Recorrido de Juan:  [1, 2, 4, 6]
Costo de Juan:  790
Recorrido de Pedro:  [1, 3, 7]
Costo de Pedro:  320
Juan visitó más ciudades
Pedro tuvo el viaje más barato
>>> 

Ejercicio: 3Eva_IIT2011_T1 Generar números 1800-nombre

resultados obtenidos

>>> teclaletra('K')
5

Instrucciones Python

# 3Eva_IIT2011_T1 Generar números 1800-nombre

def teclaletra(letra):
    letras = ['ABC','DEF','GHI',
              'JKL','MNO','PQRS',
              'TUV','WXYZ']
    tecla = [2,3,4,5,6,7,8,9]
    n = len(letras)
    equivale = 0
    for i in range(0,n,1):
        if letra in letras[i]:
            equivale = tecla[i]
    return(equivale)
    
# Tarea, desarrollar literal b

Ejercicio: 3Eva_IIT2010_T3 Rompecabezas, desordena y ubica

Incluye respuestas del tema 1 y Tema 2

Propuesta de solución en Python:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 3Eva_IIT2010_T3 Rompecabezas, desordena y ubica
# Propuesta: edelros@espol.edu.ec
# Tarea: identificar donde se podrá usar lazo "for"
# opcional, el tamaño de matriz nxm se puede obtener con
# numpy.shape(matriz) y se obtiene un arreglo con n y m

import numpy
import random

# Tema 1. funcion desordena(n)
# dado el tamaño de matriz cuadrada, pone numeros aleatorios
# No repetidos entre 0 y n*n-1
def desordena(n):
    matriz = numpy.zeros(shape=(n,n), dtype=int)
    numero = 1
    maximo = n*n-1
    while not(numero>maximo):
        fila = int(random.random()*n)+0
        columna = int(random.random()*n)+0
        if (matriz[fila,columna]==0):
            matriz[fila,columna]=numero
            numero = numero+1
    return(matriz)

# Tema 2. ubica un numero k en la matriz de nxn
def ubica(matriz,n,k):
    donde = numpy.zeros(2, dtype=int)
    encontre = 0
    fila = 0
    while not(fila>=n or encontre==1):
        columna = 0
        while not(columna>=n or encontre==1):
            if (matriz[fila,columna]==k):
                encontre = 1
                donde[0] = fila
                donde[1] = columna
            columna = columna+1
        fila = fila+1
    return(donde)

# funcion matrizigual, compara dos matrices A y B
# de igual tamano nxn
def matrizigual(A,B,n):
    resuelto = 1
    fila = 0
    while not(fila>=n or resuelto==0):
        columna = 0
        while not(columna>=n or resuelto==0):
            if (A[fila,columna]!=B[fila,columna]):
                resuelto = 0
            columna = columna+1
        fila = fila+1
    return(resuelto)

# funcion solucion del rompecabeza
# Usado para comparar con la solucion
def original(n):
    matriz = numpy.zeros(shape=(n,n), dtype=int)
    numero = 1
    fila = 0
    while not(fila>=n):
        columna = 0
        while not(columna>=n):
            matriz[fila, columna] = numero
            numero = numero+1
            columna = columna+1
        fila = fila+1
    matriz[n-1,n-1] = 0
    return(matriz)


# Tema 3. Juego del Rompecabeza
# Programa para jugar el Rompecabeza

tamano = int(input('¿Tamaño del tablero?: '))

resuelto = 0
turno = 1
solucion = original(tamano)
tablero = desordena(tamano)

while not(resuelto==1):
    print(turno)
    print(tablero)
    ficha = int(input('¿Ficha a mover?: '))
    dondeficha = ubica(tablero,tamano,ficha)
    dondecero = ubica(tablero,tamano,0)

    if (dondeficha[0]==dondecero[0] or dondeficha[1]==dondecero[1]):
        temporal = ficha
        tablero[dondeficha[0],dondeficha[1]] = 0
        tablero[dondecero[0],dondecero[1]] = temporal
    turno = turno+1
    if (matrizigual(tablero,solucion,tamano)==1):
        resuelto = 1
        print('Ganaste...! ')

Ejercicio: 3Eva_IIT2010_T2 Ubicar número dentro de una matriz

Propuesta de solución en Python

Tarea: integrar con tema 3

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 3Eva_IIT2010_T2 Ubicar número dentro de una matriz
# Propuesta: edelros@espol.edu.ec
# Tarea: integrar con tema 3

import numpy as np
import random as rnd

# Tema 2. ubica un numero k en la matriz de nxn
def ubica(matriz,k):
    tamano = np.shape(matriz)
    n = tamano[0]
    m = tamano[1]
    
    donde = np.zeros(2, dtype=int)
    encontre = 0
    fila = 0
    while not(fila>=n or encontre==1):
        columna = 0
        while not(columna>=n or encontre==1):
            if (matriz[fila,columna]==k):
                encontre = 1
                donde[0] = fila
                donde[1] = columna
            columna = columna+1
        fila = fila+1
    return(donde)

resultado del algoritmo

>>> matriz = np.array([[8, 2, 6],
		       [5, 4, 0],
                       [1, 7, 3]])
>>> ubica(matriz,7)
array([2, 1])
>>> 

Ejercicio: 3Eva_IT2010_T2 Funciones ocupados y ubica libre en matriz

resultado obtenido:

matriz = [[1,1,1,1],
          [1,0,0,0],
          [0,1,0,1]]

ocupados:  7
primer encontado:  [1, 1]
>>> 

Instrucciones en Python

# 3Eva_IT2010_T2 Funciones ocupados y ubica libre en matriz
# resolver sin usar numpy
import numpy as np

def ocupados(matriz):
    suma = np.sum(matriz)
    return(suma)

def ubicalibre(matriz):
    matriz = np.array(matriz)
    tamano = np.shape(matriz)
    n = tamano[0]
    m = tamano[1]
    encontre = 0
    a = np.NaN
    b = np.NaN
    i = 0
    while i<n and encontre==0:
        j = 0
        while j<m and encontre ==0:
            if matriz[i,j] == 0:
                encontre = 1
                a = i
                b = j
            j = j+1
        i = i + 1
    return([a,b])

# PROGRAMA
matriz = [[1,1,1,1],
          [1,0,0,0],
          [0,1,0,1]]

# PROCEDIMIENTO
aforo = ocupados(matriz)
libre = ubicalibre(matriz)

# SALIDA
print("ocupados: ", aforo)
print('primer encontado: ',libre)

Ejercicio: 3Eva_IIT2010_T1 Matriz con aleatorios no repetidos (desordena)

Propuesta de solución en Python:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 3Eva_IIT2010_T1 Matriz con aleatorios no repetidos (desordena)
# Propuesta: edelros@espol.edu.ec
# Tarea: integrar con tema 3

import numpy as np
import random as rnd

def desordena(n): 
    matriz = -1*np.ones(shape=(n,n), dtype=int)
    usados = []
    
    # entero aleatorio [0,n**2), no incluye n**2
    intervalo = n**2
    
    fila = 0
    while not(fila>=n):
        
        columna = 0
        while not(columna>=n):

            # numero no repetido
            numero = int(rnd.random()*intervalo)+0
            while numero in usados:
                numero = int(rnd.random()*intervalo)+0
            
            matriz[fila,columna] = numero
            usados.append(numero)
            
            columna = columna + 1
            
        fila = fila + 1
    return(matriz)

resultado del algoritmo:

>>> desordena(3)
array([[0, 7, 2],
       [6, 5, 8],
       [4, 1, 3]])
>>> desordena(3)
array([[7, 3, 6],
       [8, 1, 0],
       [5, 2, 4]])
>>> 

Ejercicio: 3Eva_IT2010_T1 Ecuación Verhulst

Para probar el ejercico se usa po=1, a=0.5 b=0.02 y tiempo maximo = 40

con el algoritmo se puede observar:

poblacion inicial p0:1
factor a:0.5
factor b:0.02
calcular en t:40
tiempo:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40]
pi:
[1.0, 1.6070209244539886, 2.5434661610272977, 3.9338336459524355, 5.885057578381894, 8.417395145518748, 11.39009430586252, 14.494961881174662, 17.366232541771218, 19.73763290519436, 21.51998720327935, 22.766959376324014, 23.596257413785583, 24.129351687331045, 24.464588393188883, 24.67249666532522, 24.80032998711217, 24.878512232622807, 24.92617278160938, 24.95516943765841, 24.972789690449925, 24.983489042065916, 24.98998299475044, 24.99392342119231, 24.996314016127226, 24.99776420806526, 24.998643875922703, 24.999177451612496, 24.999501092725076, 24.99969739506529, 24.999816459955184, 24.999888677013956, 24.999932479077533, 24.999959046446833, 24.999975160398368, 24.999984934014144, 24.999990862015494, 24.99999445753143, 24.99999663832259, 24.999997961039472, 24.99999876330789]
>>>

que produce la siguiente gráfica

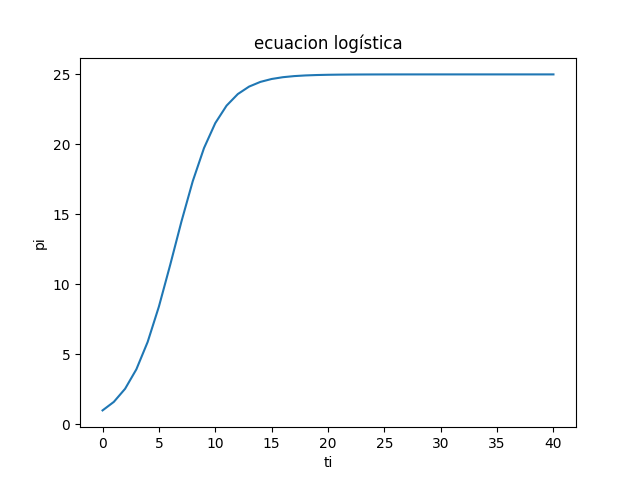
Instrucciones en Python

# 3Eva_IT2010_T1 Ecuación Verhulst
import numpy as np
import matplotlib.pyplot as plt

def f_logistica(p0,a,b,t):
    numerador = a*p0
    denominador = b*p0+(a-b*p0)*np.exp(-a*t)
    p = numerador/denominador
    return(p)

# PROGRAMA ------
# INGRESO
p0 = float(input("poblacion inicial p0:"))
a  = float(input("factor a:"))
b  = float(input("factor b:"))
t  = float(input("calcular en t:"))

# PROCEDIMIENTO
ti = []
pi = []
i = 0
while i<=t:
    pi.append(f_logistica(p0,a,b,i))
    ti.append(i)
    i = i + 1

# SALIDA
np.set_printoptions(precision=3)
print('tiempo:')
print(ti)
print('pi:')
print(pi)

# grafica
plt.plot(ti,pi)
plt.xlabel('ti')
plt.ylabel('pi')
plt.title('ecuacion logística')
plt.show()

Tarea, estimar el tiempo t cuando la población se duplica

Ejercicios: 3Eva_IT2009_T3 Aspirantes a escuela de policia

Propuesta de solución en Python: py_pdf, también con versión en matlab: m_pdf

Para resolver el problema, se usa la estructura básica para un menú y una estructura de datos con los campos de la tabla aspirante. El promedio de edad es la suma de la columna edad dividido para el número de registros. En los casos de totales por género e instrucción se usarán contadores.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 3Eva_IT2009_T3 Aspirantes a escuela de policia
# Propuesta de solucion: edelros@espol.edu.ec
# Tarea: Desarrollar caso 3, Contar por genero

import numpy as np

# Tabla usada es aspirante
aspirante = []
n = 0
opcion = 0
while not(opcion==5):
    print('1. Registra aspirante')
    print('2. Promedio de edad')
    print('3. Total por genero')
    print('4. Total por instruccion')
    print('5. Salir')
    
    opcion = int(input('cual opcion: '))
    
    if (opcion==1):
        print('  Registra aspirante')
        texto  = input('           nombre: ')
        numero = int(input('             edad: '))
        gen    = int(input('     genero [1,2]: '))
        escolar   = int(input('instruccion [1,3]: '))
        candidato = {'nombre':texto,
                     'edad':numero,
                     'genero':gen,
                     'instruccion':escolar}
        aspirante.append(candidato)
        n = n + 1
        
    if (opcion==2):
        print('  Promedio de edad')

        # n=len(aspirante)
        suma = 0
        fila = 0
        while not(fila>=n):
            suma = suma + aspirante[fila]['edad']
            fila = fila + 1
        promedio = suma/n
        print(promedio)
        
    if (opcion==3):
        print('  Total por genero')
        # TAREA: Contar por genero
        
    if (opcion==4):
        print('  Total por instruccion')
        
        # No se usará la fila 0 de veces
        veces = np.zeros(3+1,dtype=int)
        fila = 0
        while (fila<n):
            k = aspirante[fila]['instruccion']
            veces[k] = veces[k]+1
            fila = fila + 1

        # Salida
        print('   primaria: '+str(veces[1]))
        print(' segundaria: '+str(veces[2]))
        print('   superior: '+str(veces[3]))
        
    if (opcion==5):
        print(' gracias por usar el software ')

    if (opcion<1 or opcion>5):
        print(' *** NO ES OPCION DISPONIBLE ***')

ejercicios resueltos Python 3eva_it2009_t3 py_pdf

ejercicios resueltos Matlab 3eva_it2009_t3 pdf

Ejercicio: 3Eva_IT2009_T2 Seleccionar billetes de cajero automático

El algoritmo requiere la cantidad como un número entero.

 cantidad=77

Se obtiene el número de billetes por denominación como cociente de cantidad y la de nominación en forma descendente [50,20,10,5,1]

billetes50 = cantidad//50

Por cada operación anterior se debe obtener el saldo, restando el valor de los billetes por denominación por la cantidad o saldo anterior

saldo = cantidad-50*(billete50)

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 3Eva_IT2009_T2 Seleccionar billetes de cajero automático
# Propuesta en forma de programa. edelros@espol.edu.ec.

# INGRESO
cantidad = int(input('Cantidad solicitada: '))

# PROCEDIMIENTO

# cociente O división entera //
billete50 = cantidad//50
saldo     = cantidad-50*(billete50)
billete20 = saldo//20
saldo     = saldo-20*(billete20)
billete10 = saldo//10
saldo     = saldo-10*(billete10)
billete05 = saldo//5
billete01 = saldo-5*(billete05)

# Salida
print ('de 50:',billete50)
print ('de 20:',billete20)
print ('de 10:',billete10)
print ('de 05:',billete05)
print ('de 01:',billete01)

Nota: Si ha completado la unidad 4, realice el ejercicio usando un vector denominación de billetes = [50,20,10,5,1] par obtener el resultado.

Algoritmo como función, si ya ha completado la unidad 5.

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 3Eva_IT2009_T2 Seleccionar billetes de cajero automático
# Propuesta función. edelros@espol.edu.ec.
import numpy as np

def billete(cantidad):

    # division entera o cociente //
    billete50 = cantidad//50
    saldo     = cantidad - 50*(billete50)
    billete20 = saldo//20
    saldo     = saldo - 20*(billete20)
    billete10 = saldo//10
    saldo     = saldo - 10*(billete10)
    billete05 = saldo//5
    billete01 = saldo - 5*(billete05)

    # define variable de salida
    entrega    = np.array([0, 0, 0, 0, 0], int)
    entrega[0] = billete50
    entrega[1] = billete20
    entrega[2] = billete10
    entrega[3] = billete05
    entrega[4] = billete01

    return (entrega)

---

Propuesta de solución en Python: y también incluye versión en matlab

ejercicios resueltos Python 3eva_it2009_t2 pdf

ejercicios resueltos Matlab 3eva_it2009_t2 pdf