[ Escalares ] [ Vectores ] [ Matrices ] [ Listas ] || [ Operaciones ]
..
Referencia: Van Rossum 3.2 p9, Rodríguez 5.6.1 p58, Downey 2.1
1. Datos numéricos ESCALARES
Las variables numéricas de un solo valor o elemento utilizadas en un algoritmo se clasificarán en enteras, reales, complejas y lógicas.
1.1 Variables numéricas tipo entero
Es el tipo de variable usada para contar el número de estudiantes presentes en un aula de clases, pasajeros en un bus, barco o avión.
Los datos numéricos enteros indican la cantidad de elementos: una manzana, cuatro manzanas en un canasto, etc.
La variable numérica recomendada a usar en los casos es la tipo entera, pues siempre los decimales serían cero.
Ejemplo de tipo de datos numéricos enteros en Python: int()
>>> a = int(input('escriba un entero: '))
>>> b = 5
>>> c = a*b
>>> type(a)
<class 'int'>
1.2 Variables tipo Real
Este tipo de variable se usa para escribir por ejemplo el precio de un producto que incluye los centavos, el peso de un producto en Kg, el número π.
En estos casos, al escribir con decimales, se los considera como variable tipo real. Ejemplos: $9.99, $89.32, 1.268Kg, 3.1416
Ejemplo de tipo de datos numéricos reales en Python: float()
>>> g = float(input('escriba un real')
>>> valor = 3.1415927
>>> type(valor)
<class 'float'>
1.3 Variables tipo Compleja
El tipo de dato numérico usado usado para representar números complejos, aquellos que tienen parte imaginaria (raiz(-1)). En Python se definen en dos partes como: complex(real,imaginaria)
>>> w = complex(1,.5)
>>> w
(1+0.5j)
>>> type(w)
<class 'complex'>
>>> w.real
1.0
>>> w.imag
0.5
>>> w.conjugate()
(1-0.5j)
1.4 Variables tipo Booleana
Se usan en lógica matemática como valor verdadero 1 y falso 0.
Tienen aplicaciones como en asistencia a clases:
presente=0, presente=1,
y pueden sustituir símbolos como √ para asistencia y X para una ausencia de una clase.
>>> tarea = True
>>> type(tarea)
<class 'bool'>
>>> leccion = False
>>> aprender = tarea and leccion
>>> aprender
False
>>> asiste = tarea or leccion
>>> asiste
True
>>> esperanza = not(leccion)
>>> esperanza
True
>>> examen = 1
>>> leccion = 1
>>> tarea = 0
>>> aprendizaje = leccion and tarea
>>> aprendizaje
0
>>> estudia = leccion or tarea
>>> estudia
1
>>> aprueba = examen and leccion and tarea
>>> aprueba
0
Para el desarrollo de algoritmos básicos se describirán solo estos tipos numéricos como grupos principales. Para el caso de lenguajes de programación se definirán otros subtipos: entero, entero largo, real, real doble, etc. que se describirán durante el desarrollo del curso
[ Escalares ] [ Vectores ] [ Matrices ] [ Listas ] || [ Operaciones ]
..
2. VECTORES en programación
Usados por ejemplo para tabular la cantidad e manzanas en los arboles de un huerto como control de producción por árbol.
La fila de un huerto es el vector, cada árbol es el índice del vector, la cantidad de manzanas producidas es el valor de cada casilla del vector.
huerto
| árbol |
1 |
2 |
3 |
| manzanas |
15 |
18 |
17 |
tamaño del vector=3
Por ejemplo, en el huerto, el árbol con la etiqueta 2 tiene 18 manzanas.
huerto = [15,18,17]
huerto[2] = 18
En realidad en programación el primer índice será el cero, asunto a tomar en cuenta cuando se usan los índices entre la programación y el uso diario de identificadores. Es semejante cuando culturalmente se numeran los pisos de un edificio como planta baja, primer piso, segundo piso
índices = [0,1,2,..]
huerto = [15,18,17]
huerto[1] = 18
en el ejemplo el vector se encuentra formado por números enteros.
ARREGLOS
Arreglos de una dimensión o vectores, requieren importar numpy. Las librerías numpy incorporan muchas operaciones de vectores y matrices usadas en otros cursos como álgebra lineal (http://blog.espol.edu.ec/matg1049/)
Vectores – Arreglos de una dimensión
Por ejemplo: las notas de 1ra, 2da y 3ra evaluación se pueden escribir en un vector.
vector = \begin{pmatrix}7.2 \\ 8.4 \\ 9.23\end{pmatrix}
>>> import numpy as np
>>> vector = np.array([7.2, 8.4, 9.23])
>>> type(vector)
<class 'numpy.ndarray'>
Para el caso de calificaciones, se pueden usar números reales como elementos del vector.
Los vectores pueden contener escalares de tipo entero, real o complejo, como se usan en matemáticas.
El tema se desarrolla en la Unidad 4 con ejemplos y ejercicios.
[ Escalares ] [ Vectores ] [ Matrices ] [ Listas ] || [ Operaciones ]
..
2 Matrices – Arreglos de dos dimensiones
Una matriz Matriz o arreglo puede ser desde un sistema de ecuaciones, una tabla de goles de un campeonato o una hoja de calendario.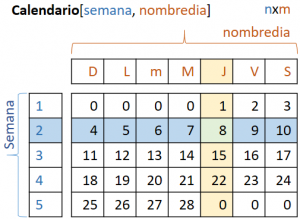 
Se usan índices para filas y columnas. Para ele ejemplo las filas representan las semanas y las columnas el nombre del día.
El valor de una casilla se determina por el nombre de la matriz y sus correspondientes fila y columna.
matriz = \begin{pmatrix}1.2 && 2.45 && 5.3 \\ 0.3 && 1.75 && 4.89\end{pmatrix}
Matrices requieren importar numpy
>>> matriz=numpy.array([[1.2, 2.45, 5.3],
[0.3, 1.75, 4.89]])
>>> type(matriz)
<class 'numpy.ndarray'>
>>> matriz
array([[ 1.2 , 2.45, 5.3 ],
[ 0.3 , 1.75, 4.89]])
las matrices de igual manera pueden contener valores de de tipo entero, real o complejo, etc. acorde al problema a realizar.
El tema se desarrolla mucho más en la unidad 4 en el enlace:
4.2 Matrices en programación – Arreglos de dos dimensiones en Python
[ Escalares ] [ Vectores ] [ Matrices ] [ Listas ] || [ Operaciones ]
..
3. LISTAS
Otra forma de agrupar datos como en vectores y matrices son las listas.
Para uso de matemáticas, cálculo numérico o álgebra lineal se recomienda usar arreglos, pues las operaciones de las librerías (numpy) están optimizadas para el uso de arreglos.
Ejemplo de un vector de números enteros como lista:
>>> vector = [1,4,2,1]
>>> type(vector)
<class 'list'>
Ejemplo de una matriz como lista:
>>> matriz = [[1,2,3,4],
[5,6,7,8]]
>>> type(matriz)
<class 'list'>
>>> matriz[0][2]
3
>>>
En el caso de vectores y matrices numéricos es preferible usar arreglos por la disponibilidad de operaciones numéricas, algebraicas disponibles en la librería Numpy.
[ Escalares ] [ Vectores ] [ Matrices ] [ Listas ] || [ Operaciones ]
