Ejercicio: 1Eva_IIIT2003_T2 Verificar números triangulares
El problema planteado es semejante a construir una pirámide, en la que se disponen de solo t bloques y se requiere saber si el número de bloques es exacto para formar una pirámide.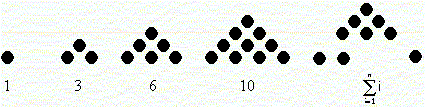
El ejercicio se desarrolla suponiendo que se construirá una pirámide con bloques de varios «pisos».
Se observa que el número de bloques coincide con el número de piso a construir.
Ejemplo:
|
piso = 1 # contador usados = 0 # acumulador |
Cada piso usa una cierta cantidad de bloques que se cuentan como «usados», es decir se acumulan. La cantidad de bloques por piso es la misma que el número del piso, contador que se inicia con 1.
El lazo o bucle repite el proceso de tal forma que los bloques usados se aumulan en cada piso.
while (usados<t):
usados = usados + piso
piso = piso+1
Dado un número t de bloques ,se calcula la secuencia de números triangulares mientras los bloques usados sean menores que los t disponibles.
En caso que el número “usados” de la secuencia es igual a t, se considera al número t como un número triangular.
La respuesta es un valor de verdad, si es triangular 1, si no lo es 0.
Lazo mientras-repita en Python
# ICM00794-Fundamentos de Computación - FCNM-ESPOL # 1Eva_IIIT2003_T2 Números triangulares # Propuesta de solución. edelros@espol.edu.ec # INGRESO t = int(input('Verificar si es triangular: ')) # PROCEDIMIENTO piso = 1 usados = 0 while (usados<t): usados = usados + piso piso = piso+1 # verifica si es triangular if usados==t: estriangular = 1 else: estriangular = 0 # SALIDA print(estriangular )
Lazo Repita-hasta en Python
# ICM00794-Fundamentos de Computación - FCNM-ESPOL # 1Eva_IIIT2003_T2 Números triangulares # Propuesta de solución. edelros@espol.edu.ec # INGRESO t = int(input('Verificar si es triangular: ')) # PROCEDIMIENTO piso = 1 usados = 0 while not(usados>=t): usados = usados+piso piso = piso+1 # verifica si es triangular if usados==t: estriangular = 1 else: estriangular = 0 # SALIDA print(estriangular )
Diagrama de Flujo
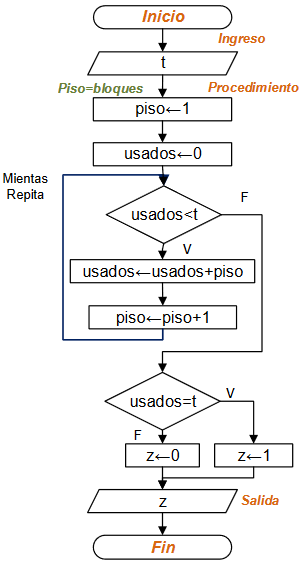
Propuesta de solución con diagrama de flujo, Python y otra versión con matlab
