Ejercicio: 2Eva_2023PAOII_T1 Volumen por solido de revolución
 El volumen se calcula a partir de la expresión:
El volumen se calcula a partir de la expresión:
V = \int_{a}^{b} \pi (f(x))^2 dx
literal a y c
Para el volumen con f(x) con al menos 3 tramos y un método de Simpson, directamente se puede usar 3/8. Por lo que se Se reemplaza en la fórmula de volumen del sólido de revolución f(x) con:
f(x) = \sqrt{\sin (x/2)}
obteniendo:
V_{fx} = \int_{a}^{b} \pi \Big(\sqrt{\sin (x/2)} \Big)^2 dx = \int_{a}^{b} \pi \sin (x/2) dx
La expresión dentro del integral se denomina como fv:
f_v (x)= \pi \sin (x/2)
en el intervalo [0.1, 1.8], con al menos 3 tramos, se requieren 4 muestras con tamaño de paso hf: y truncando a 4 decimales los resultados calculados con Python.
h_f =\frac{b-a}{tramos} = \frac{1.8-0.1}{3} = 0.5666
los puntos de muestra quedan np.linspace(0.1,1.8,3+1):
xis= [0.1, 0.6666, 1.2333, 1.8 ]
El integral se calcula con los puntos de muestra,
V_{fx} = \frac{3}{8} (0.5666) \Big( f_v(0.1) +3 f_v(0.6666) +
+ 3 f_v(1.2333)+ f_v(1.8)\Big)
recordando que se usa en radianes,
V_{fx} = \frac{3}{8} (0.5666) \Bigg( \pi \sin \Big(\frac{0.1}{2}\Big) +3 \pi \sin \Big(\frac{0.6666}{2}\Big) +
+ 3 \pi \sin\Big(\frac{1.2333}{2}\Big)+ \pi \sin \Big(\frac{1.8}{2}\Big)\Bigg)
= \frac{3}{8} (0.5666) \Big( 0.1570+3 (1.0279) +
+ 3 (1.8168)+ 2.4608\Big)
literal d. el volumen generado por f(x) tiene como resultado:
V_{fx} = 2.3698
la cota de error para fx es el orden de O(h5) = O(0.56665) = O(0.05843), queda como tarea completar la cota de error total.
literal b y c
Para el volumen con g(x) con al menos 2 tramos y Cuadratura de Gauss de dos puntos, se reemplaza en la fórmula de volumen de sólido de revolución:
g(x) = e^{x/3} - 1
V_{gx} = \int_{a}^{b} \pi (e^{x/3} - 1)^2 dx
La expresión dentro del integral se denomina como gv:
g_v = \pi (e^{x/3} - 1)^2
en el intervalo [0.1, 1.8], con al menos 2 tramos, se requieren 3 muestras con tamaño de paso hg:
h_g =\frac{b-a}{tramos} = \frac{1.8-0.1}{2} = 0.85
xic = [0.1, 0.95, 1.8 ]
tramo 1: [0.1, 0.95] , a = 0.1 , b= 0.95, truncando a 4 decimales
x_a = \frac{0.95+0.1}{2} - \frac{0.95-0.1}{2}\frac{1}{\sqrt{3}} = 0.2796
x_b = \frac{0.95+0.1}{2} + \frac{0.95-0.1}{2}\frac{1}{\sqrt{3}} = 0.7703
g_v(0.2796) = \pi (e^{0.2796/3} - 1)^2 = 0.02998
g_v(0.7703) = \pi (e^{0.7703/3} - 1)^2 = 0.2692
V_{c1} = \frac{0.95-0.1}{2}(g_v(0.2796) + g_v(0.7703))
V_{c1} = \frac{0.95-0.1}{2}(0.02998 + 0.2692)
V_{c1} = 0.1271
tramo 2: [0.95, 1.8] , a = 0.95 , b= 1.8
x_a = \frac{1.8+0.95}{2} - \frac{1.8-0.95}{2}\frac{1}{\sqrt{3}} = 1.1296
x_b = \frac{1.8+0.95}{2} - \frac{1.8-0.95}{2}\frac{1}{\sqrt{3}} = 1.6203
g_v(1.1296) = \pi (e^{1.1296/3} - 1)^2 = 0.6567
g_v(1.6203) = \pi (e^{1.6203/3} - 1)^2 = 1.6115
V_{c2} = \frac{1.8-0.95}{2}(g_v(1.1296) + g_v(1.6203))
V_{c2} = \frac{1.8-0.95}{2}(0.6567 + 1.6115)
V_{c2} = 0.9640
literal d. volumen generado por g(x)
V_{gx} = V_{c1} + V_{c2} = 0.1271 + 0.9640 = 1.0912
completar la cota de error para cuadratura de Gauss de dos puntos.
literal e. El volumen de revolución se genera como la resta del volumen de f(x) y volumen g(x)
V = V_{fx} - V_{gx} = 2.3698 - 1.0912 = 1.2785
Algoritmo con Python
Los resultados usando el algoritmo con las operaciones usadas en el planteamiento son:
para f(x):
xis= [0.1 0.66666667 1.23333333 1.8 ]
fiv= [0.15701419 1.02791246 1.81684275 2.46089406]
Volumenfx: 2.369836948864926
para g(x):
Por tramos: [0.1 0.95 1.8 ]
xab= [0.2796261355944091, 0.770373864405591,
1.129626135594409, 1.620373864405591]
gab= [0.02998177327492598, 0.26928904479784566,
0.6567986343358181, 1.6115494735531555]
Vc1= 0.12719009768092793 ; Vc2= 0.964047945852814
Volumengx: 1.0912380435337419
Volumen solido revolucion: 1.2785989053311841
Considerando realizar los cálculos para cada sección:
# 2Eva_2023PAOII_T1 Volumen por solido de revolución
import numpy as np
# INGRESO
fx = lambda x: np.sqrt(np.sin(x/2))
gx = lambda x: np.exp(x/3)-1
a = 0.1
b = 1.8
tramosSimpson = 3
tramosCGauss = 2
# PROCEDIMIENTO
# Volumen para f(x) con Simpson
fv = lambda x: np.pi*np.sin(x/2)
hs = (b-a)/tramosSimpson
xis = np.linspace(a,b,tramosSimpson +1)
fiv = fv(xis)
Vs = (3/8)*hs*(fiv[0]+3*fiv[1]+3*fiv[2]+ fiv[3])
# Volumen para g(x) con Cuadratura de Gauss
gv = lambda x: np.pi*(np.exp(x/3)-1)**2
hc = (b-a)/tramosSimpson
xic = np.linspace(a,b,tramosCGauss +1)
# tramo 1
ac = xic[0]
bc = xic[1]
xa = (bc+ac)/2 + (bc-ac)/2*(-1/np.sqrt(3))
xb = (bc+ac)/2 + (bc-ac)/2*(1/np.sqrt(3))
Vc1 = (bc-ac)/2*(gv(xa)+gv(xb))
xab = [xa,xb]
gab = [gv(xa),gv(xb)]
# tramo 2
ac = xic[1]
bc = xic[2]
xa = (bc+ac)/2 + (bc-ac)/2*(-1/np.sqrt(3))
xb = (bc+ac)/2 + (bc-ac)/2*(1/np.sqrt(3))
Vc2 = (bc-ac)/2*(gv(xa)+gv(xb))
Vc = Vc1+Vc2
xab.append(xa)
xab.append(xb)
gab.append(gv(xa))
gab.append(gv(xb))
# Volumen solido revolucion
Volumen = Vs - Vc
# SALIDA
print("para f(x):")
print("xis=", xis)
print("fiv=", fiv)
print("Volumenfx: ",Vs)
print()
print("para g(x):")
print("Por tramos:",xic)
print("xab=", xab)
print("gab=", gab)
print("Vc1=",Vc1," ; Vc2=",Vc2)
print("Volumengx: ",Vc)
print()
print("Volumen solido revolucion:",Volumen)
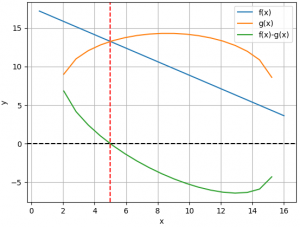
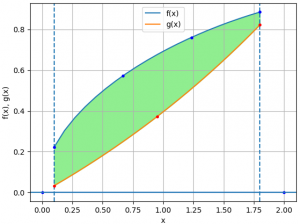
para la gráfica presentada en el enunciado (no requerida) , se complementa con las instrucciones:

# para grafica -------------------
import matplotlib.pyplot as plt
muestras = 21 # grafica
xi = np.linspace(a,b,muestras)
fi = fx(xi)
gi = gx(xi)
xig = np.linspace(a,b,tramosCGauss+1)
fis = fx(xis)
gig = gx(xig)
# grafica
plt.plot(xi,fi, label="f(x)")
plt.plot(xi,gi, label="g(x)")
plt.plot([0.0,2.0],[0,0], marker=".", color="blue")
plt.fill_between(xi,fi,gi,color="lightgreen")
plt.axhline(0)
plt.axvline(a, linestyle="dashed")
plt.axvline(b, linestyle="dashed")
plt.xlabel('x')
plt.ylabel('f(x), g(x)')
plt.legend()
plt.plot(xis,fis,'.b')
plt.plot(xig,gig,'.r')
plt.grid()
plt.show()
Gráfica de sólido de revolución en 3D
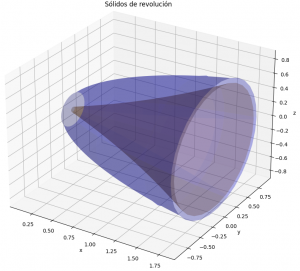
Instrucciones en Python
# 2Eva_2023PAOII_T1 Volumen por solido de revolución
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
# INGRESO
f = lambda x: np.sqrt(np.sin(x/2))
g = lambda x: np.exp(x/3)-1
# eje x
xa = 0.1
xb = 1.8
xmuestras = 31
# angulo w de rotación
w_a = 0
w_b = 2*np.pi
w_muestras = 31
# PROCEDIMIENTO
# muestreo en x y angulo w
xi = np.linspace(xa, xb, xmuestras)
wi = np.linspace(w_a, w_b, w_muestras)
X, W = np.meshgrid(xi, wi)
# evalua f(x) en 3D
Yf = f(xi)*np.cos(W)
Zf = f(xi)*np.sin(W)
# evalua g(x) en 3D
Yg = g(xi)*np.cos(W)
Zg = g(xi)*np.sin(W)
# SALIDA
# grafica 3D
figura = plt.figure()
grafica = figura.add_subplot(111, projection='3d')
grafica.plot_surface(X, Yf, Zf,
color='blue', label='f(x)',
alpha=0.3, rstride=6, cstride=12)
grafica.plot_surface(X, Yg, Zg,
color='orange', label='g(x)',
alpha=0.3, rstride=6, cstride=12)
grafica.set_title('Solidos de revolución')
grafica.set_xlabel('x')
grafica.set_ylabel('y')
grafica.set_zlabel('z')
# grafica.legend()
eleva = 45
rota = 45
deltaw = 5
grafica.view_init(eleva, rota)
# rotacion de ejes
for angulo in range(rota, 360+rota, deltaw ):
grafica.view_init(eleva, angulo)
plt.draw()
plt.pause(.001)
plt.show()