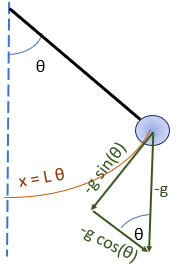
Ejercicio: 2Eva_2023PAOI_T2 Péndulo vertical amortiguado
literal a
\frac{d^2 \theta}{dt^2} = -\mu \frac{d\theta}{ dt}-\frac{g}{L}\sin (\theta)
Se simplifica su forma a:
\frac{d\theta}{dt}= z = f_t(t,\theta,z)
\frac{d^2\theta }{dt^2}= z' = -\mu z -\frac{g}{L}\sin (\theta) = g_t(t,\theta,z)
se usan los valores dados: g = 9.81 m/s2, L = 2 m
f_t(t,\theta,z) = z
g_t(t,\theta,z) = - 0.5 z -\frac{9.81}{2}\sin (\theta)
y los valores iniciales para la tabla: θ(0) = π/4 rad, θ’ (0) = 0 rad/s, se complementan los valores en la medida que se aplica el desarrollo.
| ti |
θ(ti) |
θ'(ti)=z |
| 0 |
π/4 |
0 |
| 0.2 |
0.7161 |
-0.6583 |
| 0.4 |
0.5267 |
-0.1156 |
| 0.6 |
0.2579 |
-0.1410 |
| … |
|
|
literal b
Iteración 1: ti = 0 ; yi = π/4 ; zi = 0
K1y = h * ft(ti,yi,zi)
= 0.2*(0) = 0
K1z = h * gt(ti,yi,zi)
= 0.2*(-0.5(0) -(9.81/2)sin (π/4) = -0.6930
K2y = h * ft(ti+h, yi + K1y, zi + K1z)
= 0.2*(0-0.6930)= -0.1386
K2z = h * gt(ti+h, yi + K1y, zi + K1z)
= 0.2*(-0.5(0-0.6930) -(9.81/2)sin(π/4-0)
= -0.6237
yi = yi + (K1y+K2y)/2
= π/4+ (0+(-0.1386))/2 = 0.7161
zi = zi + (K1z+K2z)/2
= 0+(-0.6930-0.6237)/2 = -0.6583
ti = ti + h = 0 + 0.2 = 0.2
estimado[i] = [0.2,0.7161,-0.6583]
Iteración 2: ti = 0.2 ; yi = 0.7161 ; zi = -0.6583
K1y = h * ft(ti,yi,zi)
= 0.2*(-0.6583) = -0.1317
K1z = h * gt(ti,yi,zi)
= 0.2*(- 0.5 ( -0.6583) -(9.81/2)sin (0.7161)
= -0.5775
K2y = h * ft(ti+h, yi + K1y, zi + K1z)
= 0.2*(-0.6583 -0.5775)= -0.2472
K2z = h * gt(ti+h, yi + K1y, zi + K1z)
= 0.2*(- 0.5 (-0.6583 -0.5775) -(9.81/2)sin(0.7161-0.1317)
= -0.4171
yi = yi + (K1y+K2y)/2
= 0.7161 + (-0.1317-0.2472)/2 = 0.5267
zi = zi + (K1z+K2z)/2
= -0.6583+(-0.5775-0.4171)/2 = -0.1156
ti = ti + h = 0.2 + 0.2 = 0.4
estimado[i] = [0.4,0.5267,-0.1156]
Iteración 3: ti = 0.4 ; yi = 0.5267 ; zi = -1.156
K1y = h * ft(ti,yi,zi)
= 0.2*(-1.156) = -0.2311
K1z = h * gt(ti,yi,zi)
= 0.2*(- 0.5(-1.156) -(9.81/2)sin (0.5267)
= -0.3771
K2y = h * ft(ti+h, yi + K1y, zi + K1z)
= 0.2*(-1.156 -0.3771)= -0.3065
K2z = h * gt(ti+h, yi + K1y, zi + K1z)
= 0.2*(- 0.5 ( -1.156 -0.3771) -(9.81/2)sin(0.5267-0.2311)
= -0.1322
yi = yi + (K1y+K2y)/2
= 0.5267 + (-0.2311-0.3065)/2 = 0.2579
zi = zi + (K1z+K2z)/2
= -1.156+(-0.3771-0.1322)/2 = -1.410
ti = ti + h = 0.4 + 0.2 = 0.6
estimado[i] = [0.6,0.2579,-1.410]
literal c
resultados del algoritmo:
[ t, y, dyi/dti=z, K1y, K1z, K2y, K2z]
[[ 0.000e+00 7.854e-01 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00]
[ 2.000e-01 7.161e-01 -6.583e-01 0.000e+00 -6.930e-01 -1.386e-01 -6.237e-01]
[ 4.000e-01 5.267e-01 -1.156e+00 -1.317e-01 -5.775e-01 -2.472e-01 -4.171e-01]
[ 6.000e-01 2.579e-01 -1.410e+00 -2.311e-01 -3.771e-01 -3.065e-01 -1.322e-01]
[ 8.000e-01 -3.508e-02 -1.377e+00 -2.820e-01 -1.089e-01 -3.038e-01 1.756e-01]
...
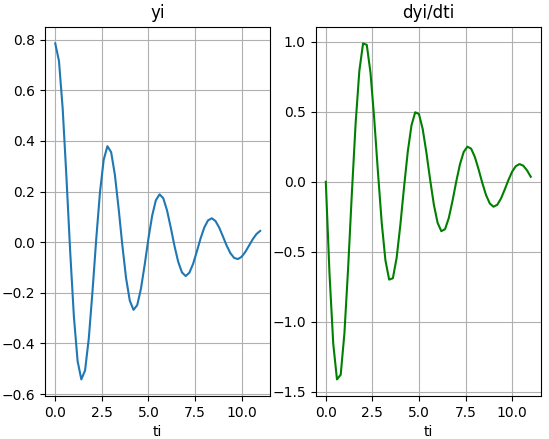
con h=0.2 se tienen 1/0.2 = 5 tramos por segundo, por lo que para 10 segundo serán 50 tramos. La cantidad de muestras = tramos + 1(valor inicial) = 51
con lo que se puede usar el algoritmo en EDO Runge-Kutta d2y/dx2
literal d
Se observa que la respuesta es oscilante y amortiguada en magnitud como se esperaba según el planteamiento. Con el tiempo se estabilizará en cero.
Instrucciones en Python
# 2Eva_2023PAOI_T2 Péndulo vertical amortiguado
import numpy as np
import matplotlib.pyplot as plt
def rungekutta2_fg(f,g,x0,y0,z0,h,muestras):
tamano = muestras + 1
estimado = np.zeros(shape=(tamano,7),dtype=float)
# incluye el punto [x0,y0,z0]
estimado[0] = [x0,y0,z0,0,0,0,0]
xi = x0
yi = y0
zi = z0
for i in range(1,tamano,1):
K1y = h * f(xi,yi,zi)
K1z = h * g(xi,yi,zi)
K2y = h * f(xi+h, yi + K1y, zi + K1z)
K2z = h * g(xi+h, yi + K1y, zi + K1z)
yi = yi + (K1y+K2y)/2
zi = zi + (K1z+K2z)/2
xi = xi + h
estimado[i] = [xi,yi,zi,K1y,K1z,K2y,K2z]
return(estimado)
# INGRESO theta = y
g = 9.8
L = 2
ft = lambda t,y,z: z
gt = lambda t,y,z: -0.5*z +(-g/L)*np.sin(y)
t0 = 0
y0 = np.pi/4
z0 = 0
h = 0.2
muestras = 51
# PROCEDIMIENTO
tabla = rungekutta2_fg(ft,gt,t0,y0,z0,h,muestras)
# SALIDA
np.set_printoptions(precision=3)
print(' [ t, \t\t y, \t dyi/dti=z, K1y,\t K1z,\t K2y,\t K2z]')
print(tabla)
# Grafica
ti = np.copy(tabla[:,0])
yi = np.copy(tabla[:,1])
zi = np.copy(tabla[:,2])
plt.subplot(121)
plt.plot(ti,yi)
plt.grid()
plt.xlabel('ti')
plt.title('yi')
plt.subplot(122)
plt.plot(ti,zi, color='green')
plt.xlabel('ti')
plt.title('dyi/dti')
plt.grid()
plt.show()
Considere dos especies de animales que ocupan el mismo ecosistema, en competencia por los recursos de alimentos y espacio definidas por:
