Ejercicio: 2Eva_IIT2017_T3 EDP parabólica con diferencias regresivas
\frac{dU}{dt} - \frac{1}{16} \frac{d^2U}{dx^2} = 0
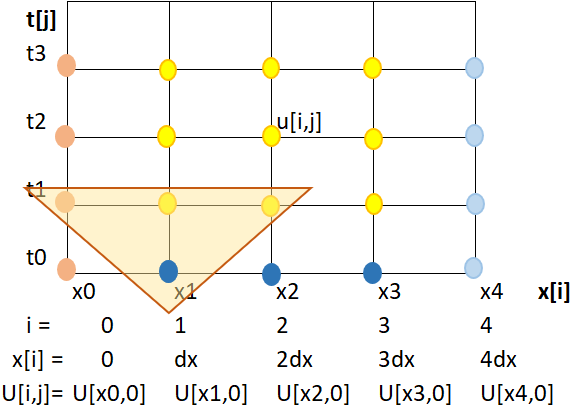
Las diferencias finitas requidas en el enunciado son:
U'(x_i,t_j) = \frac{U(x_{i},t_j)-U(x_{i},t_{j-1})}{\Delta t} + O(\Delta t)
U''(x_i,t_j) = \frac{U(x_{i+1},t_j)-2U(x_{i},t_j)+U(x_{i-1},t_j)}{\Delta x^2} + O(\Delta x^2)
La indicación de regresiva es para la primera derivada, dependiente de tiempo t.
que al reemplazar en la ecuación sin el término de error, se convierte a.
\frac{U(x_{i},t_j)-U(x_{i},t_{j-1})}{\Delta t} - \frac{1}{16}\frac{U(x_{i+1},t_j)-2U(x_{i},t_j)+U(x_{i-1},t_j)}{\Delta x^2} =0
Se reordenan los términos de forma semejante al modelo planteado en el método básico:
\frac{\Delta t}{16\Delta x^2}[U(x_{i+1},t_j)-2U(x_{i},t_j)+U(x_{i-1},t_j)] = U(x_{i},t_j)-U(x_{i},t_{j-1})
Se simplifica haciendo que haciendo
\lambda = \frac{\Delta t}{16\Delta x^2}
Cambiando la nomenclatura con solo los índices para las variables x y t, ordenando en forma ascendente los índices previo a crear el algoritmo.
\lambda[U(i+1,j)-2U(i,j)+U(i-1,j)] = U(i,j)-U(i,j-1)
Se reordena la ecuación como modelo para el sistema de ecuaciones.
\lambda U(i+1,j)+(-2\lambda-1)U(i,j)+ \lambda U(i-1,j) = -U(i,j-1)
P U(i-1,j) + Q U(i,j) + R U(i+1,j) = -U(i,j-1)
Se calculan los valores constantes:
λ = dt/(16*dx2) = 0.05/[16*(1/3)2] = 0.028125
P = λ = 0.028125
Q = (-1-2λ) = (1-2*0.028125) = -1.05625
R = λ = 0.028125
Usando las condiciones del problema:
U(0,t) = U(1,t) = 0, entonces, Ta = 0, Tb = 0
Para los valores de la barra iniciales se debe usar un vector calculado como 2sin(π x) en cada valor de xi espaciados por hx = 1/3, x entre [0,1]
xi = [0,1/3, 2/3, 1]
U[xi,0] = [2sin (0*π), 2sin(π/3), 2sin(2π/3), 2sin(π)]
U[xi,0] = [0, 2sin(π/3), 2sin(2π/3), 0]
U[xi,0] = [0, 1.732050, 1.732050, 0]
Con lo que se puede plantear las ecuaciones:
j=1: i=1
0.028125 U(0,1) + (-1.05625) U(1,1) + 0.028125 U(2,1) = -U(1,0)
j=1: i=2
0.028125 U(1,1) + (-1.05625) U(2,1) + 0.028125 U(3,1) = -U(2,0)
y reemplazando los valores de la malla conocidos:
0.028125 (0) – 1.05625 U(1,1) + 0.028125 U(2,1) = -1.732050
0.028125 U(1,1) – 1.05625 U(2,1) + 0.028125 (0) = -1.732050
hay que resolver el sistema de ecuaciones:
-1.05625 U(1,1) + 0.028125 U(2,1) = -1.732050
0.028125 U(1,1) - 1.05625 U(2,1) = -1.732050
A = [[-1.05625 , 0.028125],
[ 0.028125, -1.05625 ]]
B = [-1.732050,-1.732050]
que resuelta con un método numérico:
[ 1.68, 1.68]
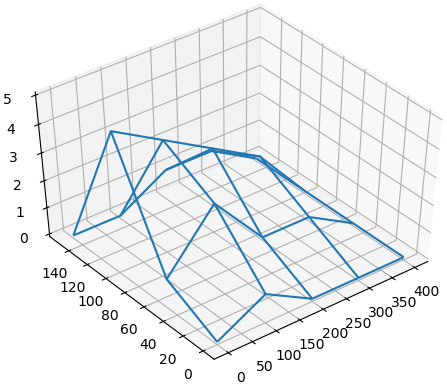
Por lo que la solución para una gráfica, con los índices de (fila,columna) como (t,x):
U = [[0, 1.732050, 1.732050, 0],
[0, 1.680000, 1,680000, 0]]
El error del procedimiento, tal como fué planteado es del orden de O(Δt) y O(Δx2), o error de truncamiento E = O(Δx2) + O(Δt). Δt debe ser menor que Δx en aproximadamente un orden de magnitud
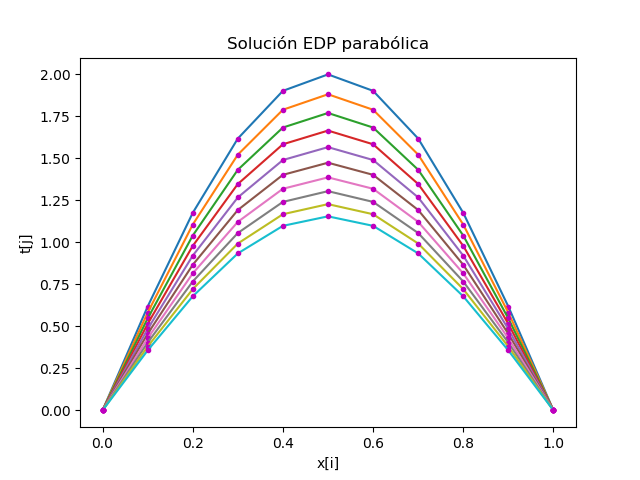
Usando algoritmo en python.
Usando lo resuelto en clase y laboratorio, se comprueba la solución con el algoritmo, con hx y ht mas pequeños y más iteraciones:
# EDP parabólicas d2u/dx2 = K du/dt
# método implícito
# Referencia: Chapra 30.3 p.895 pdf.917
# Rodriguez 10.2.5 p.417
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
# Valores de frontera
Ta = 0
Tb = 0
# longitud en x
a = 0
b = 1
# Constante K
K = 16
# Tamaño de paso
dx = 0.1
dt = 0.01
# temperatura en barra
tempbarra = lambda x: 2*np.sin(np.pi*x)
# iteraciones
n = 100
# PROCEDIMIENTO
# Valores de x
xi = np.arange(a,b+dx,dx)
m = len(xi)
# Resultados en tabla de u
u = np.zeros(shape=(m,n), dtype=float)
# valores iniciales de u
j=0
u[0,j] = Ta
for i in range(1,m-1,1):
u[i,j] = tempbarra(xi[i])
u[m-1,j] = Tb
# factores P,Q,R
lamb = dt/(K*dx**2)
P = lamb
Q = -1 -2*lamb
R = lamb
vector = np.array([P,Q,R])
tvector = len(vector)
# Calcula U para cada tiempo + dt
j=1
while not(j>=n):
u[0,j] = Ta
u[m-1,j] = Tb
# Matriz de ecuaciones
tamano = m-2
A = np.zeros(shape=(tamano,tamano), dtype = float)
B = np.zeros(tamano, dtype = float)
for f in range(0,tamano,1):
for c in range(0,tvector,1):
c1 = f+c-1
if(c1>=0 and c1<tamano):
A[f,c1] = vector[c]
B[f] = -u[f+1,j-1]
B[0] = B[0]-P*u[0,j]
B[tamano-1] = B[tamano-1]-R*u[m-1,j]
# Resuelve sistema de ecuaciones
C = np.linalg.solve(A, B)
# copia resultados a u[i,j]
for f in range(0,tamano,1):
u[f+1,j] = C[f]
j=j+1 # siguiente iteración
# SALIDA
print('Tabla de resultados')
np.set_printoptions(precision=2)
print(u)
# Gráfica
salto = int(n/10)
if (salto == 0):
salto = 1
for j in range(0,n,salto):
vector = u[:,j]
plt.plot(xi,vector)
plt.plot(xi,vector, '.m')
plt.xlabel('x[i]')
plt.ylabel('t[j]')
plt.title('Solución EDP parabólica')
plt.show()