Referencia: Chapra 23.1 p668 pdf692, Rodriguez 8.2 p324

Como referencia, el polinomio de Taylor muestra una aproximación de una función f(x):

P_{n}(x) = f(x_0)+\frac{f'(x_0)}{1!} (x-x_0) + + \frac{f''(x_0)}{2!}(x-x_0)^2 + ...

---

Primera Derivada con Diferencias divididas hacia adelante

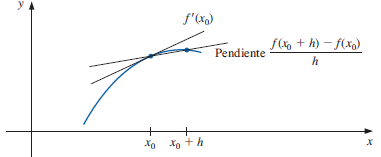
Una aproximación a primera derivada, usa los primeros dos términos del polinomio de Taylor alrededor de x_i en para un punto a la derecha x_i+1 a una distancia h = x_i+1–x_i

f(x_{i+1}) = f(x_i)+\frac{f'(x_i)}{1!} (h) + \frac{f''(x_i)}{2!}(h)^2 + ...

se puede simplificar en un polinomio de grado uno y un término de error:

f_{i+1} = f_i + f'_i (h) + O(h^2) ...

Despejando la expresión para f’_i

---

f'_i = \frac{f_{i+1}-f_i}{h} = \frac{\Delta f_i}{h}

---

La expresión también es la primera diferencia finita dividida con un error del orden O(h). (tema usado en interpolación).

Revise que el término de la expresión queda O(h²)/h con lo que se disminuye el exponente en uno.

---

Primera derivada con diferencias divididas centradas

Se realiza el mismo procedimiento que el anterior, usando un punto x_i+1 y x_i-1 alrededor de x_i. En el término x_i-1 el valor de h es negativo al invertir el orden de la resta.

f_{i+1} = f_i+\frac{f'_i}{1!}(h) + \frac{f''_i}{2!}(h)^2 f_{i-1} = f_i-\frac{f'_i}{1!}(h) + \frac{f''_i}{2!}(h)^2

restando la ecuaciones se tiene que

f_{i+1} - f_{i-1} = f'_i (h)+f'_i (h) f_{i+1} - f_{i-1} = 2h f'_i

La expresión de primera derivada usando un punto antes y otro después del punto central queda como:

---

f'_i = \frac{f_{i+1} - f_{i-1}}{2h}

---

con un error del orden O(h²)

---

---

Segundas derivadas

Al continuar con el procedimiento mostrado se pueden obtener las fórmulas para segundas derivadas, las que se resumen en las tablas de Fórmulas de diferenciación por diferencias divididas.