6.2 EDO Runge-Kutta 2do Orden dy/dx

Referencia: Burden 5.4 p272 pdf282, Chapra 25.3 p740 pdf164, Rodriguez 9.1.7 p354, Boyce DiPrima 4Ed 8.4 p450

Como tema de introducción observar dos minutos del video sugerido a partir de donde se encuentra marcado el enlace. En este caso, en combate aereo, las armas se encuentran fijas en las alas.

Video Revisar:

Luego de observar el video de introducción conteste las siguientes preguntas:
¿ Que trayectoria siguen los proyectiles al salir del cañon?
¿ Que trayectoria siguen los aviones, el perseguido y el que caza?
¿ Cuál es la relación entre las trayectorias de los dos aviones?

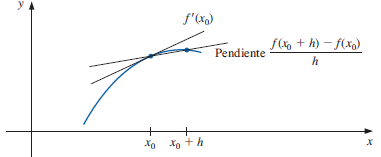
Los métodos de Runge-Kutta mejoran la aproximación a la respuesta sin requerir determinar las expresiones de las derivadas de orden superior. Los métodos usan una corrección a la derivada tomando valores de puntos alrededor referenciado al tamaño de paso h.

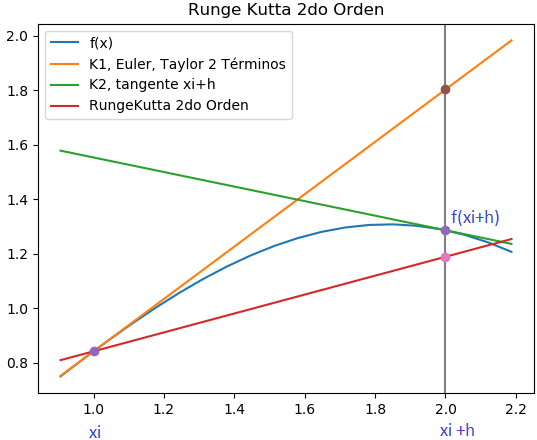Por ejemplo, Runge-Kutta de 2do Orden usa el promedio entre los incrementos xi y xi+h, calculados como términos K1 y K2.

Runge-Kutta 2do Orden tiene error de truncamiento O(h³)

# EDO. Método de RungeKutta 2do Orden 
# estima la solucion para muestras espaciadas h en eje x
# valores iniciales x0,y0
# entrega arreglo [[x,y]]
import numpy as np

def rungekutta2(d1y,x0,y0,h,muestras):
    tamano   = muestras + 1
    estimado = np.zeros(shape=(tamano,2),dtype=float)
    # incluye el punto [x0,y0]
    estimado[0] = [x0,y0]
    xi = x0
    yi = y0
    for i in range(1,tamano,1):
        K1 = h * d1y(xi,yi)
        K2 = h * d1y(xi+h, yi + K1)

        yi = yi + (K1+K2)/2
        xi = xi + h
        
        estimado[i] = [xi,yi]
    return(estimado)

Ejercicio

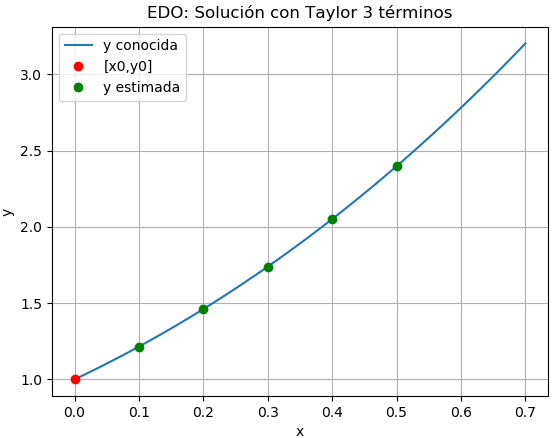
Para probar el algoritmo se usa la ecuación del problema presentado en ‘EDO con Taylor‘ :

y'-y -x +x^2 -1 = 0

que aplicado con Runge Kutta, se obtiene:

estimado[xi,yi]
[[ 0.          1.        ]
 [ 0.1         1.2145    ]
 [ 0.2         1.4599725 ]
 [ 0.3         1.73756961]
 [ 0.4         2.04856442]
 [ 0.5         2.39436369]]
Error máximo estimado:  0.00435758459732
entre puntos: 
[ 0.          0.00067092  0.00143026  0.0022892   0.00326028  0.00435758]
>>>

Compare los resultados con Taylor de 2 y 3 términos.

Los resultados se muestran también en la gráfica:

Se adjunta el programa de prueba que usa la función rungekutta2(d1y,x0,y0,h,muestras) :

# PROGRAMA PRUEBA
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1

# INGRESO
# d1y = y' = f, d2y = y'' = f'
d1y = lambda x,y: y -x**2 + x + 1
x0 = 0
y0 = 1
h  = 0.1
muestras = 5

# PROCEDIMIENTO
puntosRK2 = rungekutta2(d1y,x0,y0,h,muestras)
xi = puntosRK2[:,0]
yiRK2 = puntosRK2[:,1]

# SALIDA
print('estimado[xi,yi]')
print(puntosRK2)

Si la solución analítica es conocida, se puede añadir para comparar resultados:

# ERROR vs solución conocida
y_sol = lambda x: ((np.e)**x) + x + x**2

yi_psol  = y_sol(xi)
errores  = yi_psol - yiRK2
errormax = np.max(np.abs(errores))

# SALIDA
print('Error máximo estimado: ',errormax)
print('entre puntos: ')
print(errores)

# GRAFICA [a,b+2*h]
a = x0
b = h*muestras+2*h
muestreo = 10*muestras+2
xis = np.linspace(a,b,muestreo)
yis = y_sol(xis)

La grafica se construye como

# Gráfica
import matplotlib.pyplot as plt

plt.plot(xis,yis, label='y conocida')
plt.plot(xi[0],yiRK2[0],
         'o',color='r', label ='[x0,y0]')
plt.plot(xi[1:],yiRK2[1:],
         'o',color='m',
         label ='y Runge-Kutta 2 Orden')

plt.title('EDO: Solución con Runge-Kutta 2do Orden')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()

2017-10-062023-02-04

6.1 EDO con Taylor

Referencia: ejemplo Rodriguez 9.1.1 p335. Chapra 25.1.3 p731 pdf755

En los métodos con Taylor para Ecuaciones Diferenciales Ordinarias (EDO), se aproxima el resultado a n términos de la serie, para lo cual se ajusta la expresión del problema a la derivada correspondiente.

Ejemplo:

Se pide encontrar puntos de la solución en la ecuación diferencial usando los tres primeros términos de la serie de Taylor con h=0.1 y punto inicial x₀=0, y₀=1

y'-y -x +x^2 -1 = 0

La solución empieza usando la Serie de Taylor para tres términos:

y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i

x_{i+1} = x_{i} + h

E = \frac{h^3}{3!} y'''(z) = O(h^3)

Luego, al despejar de la fórmula planteada el valor de y’, se puede obtener y" a combinar las ecuaciones.

y' = y -x^2 +x +1

y'' = y' -2x + 1

= (y -x^2 +x +1) -2x + 1

y'' = y -x^2 -x +2

ecuaciones que permiten estimar nuevos valores y_i+1 para nuevos puntos muestra distanciados en i*h desde el punto inicial.

Se empieza evaluando el nuevo punto a una distancia x₁= x₀+h del punto de origen con lo que se obtiene y₁ , repitiendo el proceso para el siguiente punto en forma sucesiva

Algoritmo con Python

Para simplificar los calculos se crea una función edo_taylor3t() para encontrar los valores para una cantidad de muestras distanciadas entre si h veces del punto inicial [x₀,y₀]

# EDO. Método de Taylor 3 términos 
# estima solucion para muestras separadas h en eje x
# valores iniciales x0,y0
# entrega arreglo [[x,y]]
import numpy as np

def edo_taylor3t(d1y,d2y,x0,y0,h,muestras):
    tamano = muestras + 1
    estimado = np.zeros(shape=(tamano,4),dtype=float)
    # incluye el punto [x0,y0]
    estimado[0] = [x0,y0,0,0]
    x = x0
    y = y0
    for i in range(1,tamano,1):
        estimado[i-1,2:]= [d1y(x,y),d2y(x,y)]
        y = y + h*d1y(x,y) + ((h**2)/2)*d2y(x,y)
        x = x+h
        estimado[i,0:2] = [x,y]
    return(estimado)

La función se puede usar en un programa que plantee resolver el problema propuesto:

# PROGRAMA PRUEBA
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1

# INGRESO.
# d1y = y', d2y = y''
d1y = lambda x,y: y -x**2 + x + 1
d2y = lambda x,y: y -x**2 - x + 2
x0 = 0
y0 = 1
h = 0.1
muestras = 5

# PROCEDIMIENTO
puntos = edo_taylor3t(d1y,d2y,x0,y0,h,muestras)
xi = puntos[:,0]
yi = puntos[:,1]

# SALIDA
print('estimado[xi, yi, d1yi, d2yi]')
print(puntos)

obteniendo como resultados:

estimado[xi,yi]
[[ 0.          1.        ]
 [ 0.1         1.215     ]
 [ 0.2         1.461025  ]
 [ 0.3         1.73923262]
 [ 0.4         2.05090205]
 [ 0.5         2.39744677]]

Cálculo de Error

La ecuación diferencial ordinaria del ejercicio tiene una solución conocida, lo que permite encontrar el error real en cada punto respecto a la aproximación estimada.

y = e^x + x + x^2

Note que el error crece al distanciarse del punto inicial

# ERROR vs solución conocida
y_sol = lambda x: ((np.e)**x) + x + x**2

yi_psol = y_sol(xi)
errores = yi_psol - yi
errormax = np.max(np.abs(errores))

# SALIDA
print('Error máximo estimado: ',errormax)
print('entre puntos: ')
print(errores)

con los siguientes resultados:

Error máximo estimado:  0.0012745047595
entre puntos: 
[ 0.  0.000170  0.000377  0.000626  0.000922  0.00127 ]

Gráfica

Para visualizar los resultados se usan los puntos estimados y muchos más puntos para la solución conocida en el intervalo de estudio. Con la gráfica se podrán observar las diferencias entre las soluciones encontradas.

# GRAFICA [a,b+2*h]
a = x0
b = h*muestras+2*h
muestreo = 10*muestras+2
xis = np.linspace(a,b,muestreo)
yis = y_sol(xis)

# Gráfica
import matplotlib.pyplot as plt
plt.plot(xis,yis, label='y conocida')
plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]')
plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada')
plt.title('EDO: Solución con Taylor 3 términos')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()

Tarea: Realizar el ejercicio con más puntos muestra, donde se visualice que el error aumenta al aumentar la distancia del punto inicial [x₀,y₀]

2017-10-062023-02-04

Unidad 06 EDO – Ecuaciones Diferenciales Ordinarias

EDO usando polinomio de Taylor

Runge Kutta para primera derivada

Runge Kutta para segunda derivada

Sistemas EDO

2017-10-052024-08-11

5.6 Diferenciación numérica – Tablas con diferencias divididas

Referencia: Chapra Fig.23.1 pag.669 pdf.693, Burden 4.1 p167, Rodríguez 8.2,3,4,6 p324

Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]

Diferencias divididas hacia adelante

Primera derivada

f'(x_i) = \frac{f(x_{i+1})-f(x_i)}{h} + O(h)

f'(x_i) = \frac{-f(x_{i+2})+4f(x_{i+1})-3f(x_i)}{2h} + O(h^2)

Segunda derivada

f''(x_i) = \frac{f(x_{i+2})-2f(x_{i+1})+f(x_i)}{h^2} + O(h)

f''(x_i) = \frac{-f(x_{i+3})+4f(x_{i+2})-5f(x_{i+1})+2f(x_i)}{h^2}

+ O(h^2)

Tercera derivada

f'''(x_i) = \frac{f(x_{i+3})-3f(x_{i+2})+3f(x_{i+1})-f(x_i)}{h^3}

+ O(h)

f'''(x_i) = \frac{-3f(x_{i+4})+14f(x_{i+3})-24f(x_{i+2})+18f(x_{i+1})-5f(x_i)}{2h^3}

+ O(h^2)

Cuarta derivada

f''''(x_i) = \frac{f(x_{i+4})-4f(x_{i+3})+6f(x_{i+2})-4f(x_{i+1})+f(x_i)}{h^3}

+ O(h)

Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]

Diferencias divididas centradas

Primera derivada

f'(x_i) = \frac{f(x_{i+1})-f(x_{i-1})}{2h} + O(h^2)

f'(x_i) = \frac{-f(x_{i+2})+8f(x_{i+1})-8f(x_{i-1}) +f(x_{i-2})}{12h}

+ O(h^4)

Segunda derivada

f''(x_i) = \frac{f(x_{i+1})-2f(x_{i})+f(x_{i-1})}{h^2} + O(h^2)

f''(x_i) = \frac{-f(x_{i+2})+16f(x_{i+1})-30f(x_{i})+16f(x_{i-1})-f(x_{i-2})}{12h^2}

+ O(h^4)

Tercera derivada

f'''(x_i) = \frac{f(x_{i+2})-2f(x_{i+1})+2f(x_{i-1})-f(x_{i-2})}{2h^3}

+ O(h^2)

f'''(x_i) = \frac{-f(x_{i+3})+8f(x_{i+2})-13f(x_{i+1})+13f(x_{i-1})-8f(x_{i-2})+f(x_{i-3})}{8h^3}

+ O(h^4)

Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]

Diferencias divididas hacia atrás

Primera derivada

f'(x_i) = \frac{f(x_{i})-f(x_{i-1})}{h} + O(h)

f'(x_i) = \frac{3f(x_{i})-4f(x_{i-1})+f(x_{i-2})}{2h}

+ O(h^2)

Segunda derivada

f''(x_i) = \frac{f(x_{i})-2f(x_{i-1})+f(x_{i-2})}{h^2} + O(h)

f''(x_i) = \frac{2f(x_{i})-5f(x_{i-1})+4f(x_{i-2})-f(x_{i-3})}{h^2}

+ O(h^2)

Tercera derivada

f'''(x_i) = \frac{f(x_{i})-3f(x_{i-1})+3f(x_{i-2})-f(x_{i-3})}{h^3} + O(h)

f'''(x_i) = \frac{5f(x_{i})-18f(x_{i-1})+24f(x_{i-2})-14f(x_{i-3})+3f(x_{i-4})}{2h^3}

+ O(h^2)

Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]

2017-10-052024-08-11

5.5 Diferenciación numérica

Referencia: Chapra 23.1 p668 pdf692, Rodriguez 8.2 p324

Como referencia, el polinomio de Taylor muestra una aproximación de una función f(x):

P_{n}(x) = f(x_0)+\frac{f'(x_0)}{1!} (x-x_0) +

+ \frac{f''(x_0)}{2!}(x-x_0)^2 + ...

Diferencias Divididas [ hacia adelante ] [ centradas ]

Primera Derivada con Diferencias divididas hacia adelante

Una aproximación a primera derivada, usa los primeros dos términos del polinomio de Taylor alrededor de x_i en para un punto a la derecha x_i+1 a una distancia h = x_i+1–x_i

f(x_{i+1}) = f(x_i)+\frac{f'(x_i)}{1!} (h) + \frac{f''(x_i)}{2!}(h)^2 + ...

se puede simplificar en un polinomio de grado uno y un término de error:

f_{i+1} = f_i + f'_i (h) + O(h^2) ...

Despejando la expresión para f’_i

f'_i = \frac{f_{i+1}-f_i}{h} = \frac{\Delta f_i}{h}

La expresión también es la primera diferencia finita dividida con un error del orden O(h). (tema usado en interpolación).

Revise que el término de la expresión queda O(h²)/h con lo que se disminuye el exponente en uno.

Diferencias Divididas [ hacia adelante ] [ centradas ]

Primera derivada con diferencias divididas centradas

Se realiza el mismo procedimiento que el anterior, usando un punto x_i+1 y x_i-1 alrededor de x_i. En el término x_i-1 el valor de h es negativo al invertir el orden de la resta.

f_{i+1} = f_i+\frac{f'_i}{1!}(h) + \frac{f''_i}{2!}(h)^2

f_{i-1} = f_i-\frac{f'_i}{1!}(h) + \frac{f''_i}{2!}(h)^2

restando la ecuaciones se tiene que

f_{i+1} - f_{i-1} = f'_i (h)+f'_i (h)

f_{i+1} - f_{i-1} = 2h f'_i

La expresión de primera derivada usando un punto antes y otro después del punto central queda como:

f'_i = \frac{f_{i+1} - f_{i-1}}{2h}

con un error del orden O(h²)

Diferencias Divididas [ hacia adelante ] [ centradas ]

Segundas derivadas

Al continuar con el procedimiento mostrado se pueden obtener las fórmulas para segundas derivadas, las que se resumen en las tablas de Fórmulas de diferenciación por diferencias divididas.

2017-10-052024-08-11

5.4.1 Cuadratura con dos puntos – Experimento

Para visualizar el concepto de Cuadratura de Gauss de dos puntos considere lo siguiente:

Se tiene un corte transversal del un recipiente rectangular lleno de líquido limitado en x entre [-1,1], al que se le ha depositado encima otro recipiente con perfil f(x) = x² hasta que reposan sus extremos en x[-1,1].

La altura de ambos recipientes es la misma.

La superficie entre f(x) y el eje x es el integral de f(x) en el intervalo.

Si suponemos que la figura es el corte transversal de una vasija y la parte en amarillo es líquida, la vasija ha desplazado el líquido que ocupa ahora el «área» mostrada en la gráfica que corresponde al integral de f(x)=x². entre [-1,1].

Ahora, suponga que se perfora el perfil de f(x) en dos puntos equidistantes cercanos x=0. Los orificios permitirían el desplazamiento del liquido al interior de f(x) que dejando pasar suficiente tiempo, permitiría tener todo el líquido en el recipiente rectangular entre [-1,1] como una línea horizontal.

Podría medir la altura que tiene el líquido y que tiene un equivalente en un punto f(x1). Debería encontrar el valor de x1 que permite disponer del mismo valor entre el área debajo de f(x) y el rectángulo del corte transversal amarillo ahora formado.

Se usa el resultado analítico del integral restando el área del rectángulo obtenido al evaluar la función f(x) entre [0,1], teniendo un problema de búsqueda de raíces. Obtenemos el valor de x1.

Se muestra que el área bajo f(x) es equivalente al área del rectángulo conformado.

Si utilizamos el desplazamiento horizontal desde el centro para un punto encontrado como un «factor», tendremos que el área del rectángulo se mantendría equivalente, y el desplazamiento proporcional a la mitad del intervalo si se varía el intervalo de observación. Este factor coincide con el factor de Cuadratura de Gauss de dos puntos.

funcion  fx:   x**2
Integral Fx:   x**3/3
I analitico:   0.6666666666666666
I aproximado:  0.6666666666654123
desplaza centro:   0.5773502691890826
factor desplaza:   0.5773502691890826
Factor CuadGauss:  0.5773502691896258
erradoFactor:    1.2545520178264269e-12
error integral:  1.2543299732215019e-12

El error del integral es del orden de 10^-12

Cambiamos la figura geométrica a un trapecio generado por la recta que pasa por los puntos xi desplazados desde el centro.

Usamos la función f(x) = x² + x + 1, observaremos si los resultado son equivalentes.

La figura al inicio del experimento será:

Luego de realizar realizar el mismo cálculo anterior usando un equivalente a trapecio se tiene:

con valores numéricos:

funcion  fx:   x**2 + x + 1
Integral Fx:   x**3/3 + x**2/2 + x
I analitico:   2.6666666666666665
I aproximado:  2.6666666666654124
desplaza centro:   0.5773502691890826
factor desplaza:   0.5773502691890826
Factor CuadGauss:  0.5773502691896258
erradoFactor:    1.2545520178264269e-12
error integral:  1.2541079286165768e-12

El error del integral es también del orden de 10^-12, además observe que el factor de cuadratura de Gauss se mantiene.

Tarea

Realice el experimento usando un polinomio de grado superior y observe los errores para el integral y las diferencia con el coeficiente de Cuadratura de 2 puntos.

Algoritmo con Python

Para resumir la cantidad de instrucciones, se usa el método de la bisección desde la librería scipy y el subgrupo de funciones de optimización.

Los cálculos para realizar las gráficas se tratan en un bloque luego de mostrar los resultado principales.

# Integración: Cuadratura de Gauss de dos puntos
# modelo con varios tramos entre [a,b]
# para un solo segmento.
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import scipy.optimize as op

# INGRESO
x = sym.Symbol('x')

# fx = (x)**2
fx = x**2 + x + 1
# fx = 0.2 + 25.0*x-200*(x**2)+675.0*(x**3)-900.0*(x**4)+400.0*(x**5)

a = -1
b = 1
muestras = 51
tolera = 1e-12
iteramax = 100

# PROCEDIMIENTO
# Desarrollo analítico con Sympy
Fx = sym.integrate(fx,x)
Fxn = sym.lambdify('x',Fx,'numpy')
Fiab = Fxn(b)-Fxn(a)

# Busca igualar trapecio con Integral analitico
fxn = sym.lambdify('x',fx,'numpy')
base = b-a
mitad = base/2
xc = (a+b)/2  # centro
diferencia = lambda x: Fiab-base*(fxn(xc-x)+fxn(xc+x))/2
desplazado =  op.bisect(diferencia,0,mitad,
                        xtol=tolera,maxiter=iteramax)
factor = desplazado/mitad

# Integral aproximando con trapecio
x0 = xc - factor*mitad
x1 = xc + factor*mitad
Faprox = base*(fxn(x0)+fxn(x1))/2

# Integral cuadratura Gauss
xa = xc + mitad/np.sqrt(3)
xb = xc - mitad/np.sqrt(3)
FcuadG = base*(fxn(xa)+fxn(xb))/2
erradofactor = np.abs(FcuadG - Faprox)
erradoIntegral = np.abs(Fiab-Faprox)
# SALIDA
print('funcion  fx:  ', fx)
print('Integral Fx:  ', Fx)
print('I analitico:  ', Fiab)
print('I aproximado: ', Faprox)
print('desplaza centro:  ', desplazado)
print('factor desplaza:  ', factor)
print('Factor CuadGauss: ', 1/np.sqrt(3))
print('erradoFactor:   ', erradofactor)
print('error integral: ', erradoIntegral) 

# Grafica
# Para GRAFICAR 
# Para gráfica f(x)
xi = np.linspace(a,b,muestras)
fi = fxn(xi)

# Para gráfica Trapecio
m = (fxn(x1)-fxn(x0))/(x1-x0)
trapeciof = lambda x: fxn(x0)+m*(x-x0)
trapecioi = trapeciof(xi)

# Areas Trapecio para cada punto que busca
k = int(muestras/2)
xicg = xi[k:muestras-1]
Fcg = [base*(fxn(xi[k+0])+fxn(xi[k-0]))/2]
for i in range(1,k,1):
    untrapecio = base*(fxn(xi[k+i])+fxn(xi[k-i]))/2
    Fcg.append(untrapecio)

# Punto buscado
Fiaprox = base*(fxn(x1)+fxn(x0))/2

Fi = Fxn(xi)-Fxn(a)

# Areas de curvas y trapecio

plt.subplot(211) # Grafica superior
plt.xlim(a,b)
plt.plot(xi, fi, label='f(x)')
# Solo fi
# plt.fill_between(xi,0, fi,
#                label='integral fi',
#                 color='yellow')
# usando cuadratura
plt.fill_between(xi,0, trapecioi,
                 label='Cuadratura 2 puntos',
                 color='yellow')
plt.axvline(x0,color='white')
plt.axvline(x1,color='white')
plt.plot([x0,x1],[fxn(x0),fxn(x1)],
         'ro', label='x0,x1')
plt.axvline(0,color='black')
plt.xlabel('x')
plt.ylabel('f(x) y Cuadratura de 2 puntos')
plt.legend()

# Valores de integrales
plt.subplot(212) # Grafica inferior
plt.xlim(a,b)
plt.axhline(Fiab, label='F[a,b]')
# plt.plot(xi,Fi,label='F(x)')
plt.plot(xicg,Fcg,color='orange',label='Aprox Trapecio')

plt.axvline(x1,color='yellow')
plt.axvline((1/np.sqrt(3))*(b-a)/2 + xc ,color='magenta')
plt.plot(x1,Fiaprox,'ro', label='x0,x1')
plt.axvline(0,color='black')

plt.xlabel('x')
plt.legend()
plt.ylabel('Integrando')
plt.show()

2017-10-052024-08-11

5.4 Cuadratura de Gauss con Python

Referencia: Chapra 22.3 p655 pdf679, Rodriguez 7.3 p294, Burden 4.7 p220 pdf230

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Cuadratura de Gauss

La cuadratura de Gauss aproxima el integral de una función en un intervalo [a,b] centrado en cero mediante un cálculo numérico con menos operaciones y evaluaciones de la función. Se representa como una suma ponderada:

I \cong c_0f(x_0) + c_1f(x_1)

para la fórmula de dos puntos con referencia a una función centrada en cero y ancho unitario a cada lado, se tiene obtiene:

c_0 = c_1 = 1

x_0 = -\frac{1}{\sqrt{3}}, x_1 = \frac{1}{\sqrt{3}}

para un intervalo de evaluación desplazado en el eje x se requiere convertir los puntos al nuevo intervalo. Se desplaza el punto cero al centro del intervalo [a,b] y se corrige el desplazamiento hacia la izquierda y derecha del centro.

x_a = \frac{b+a}{2} - \frac{b-a}{2}\Big(\frac{1}{\sqrt{3}} \Big)

x_b = \frac{b+a}{2} + \frac{b-a}{2}\Big(\frac{1}{\sqrt{3}} \Big)

con lo que el resultado aproximado del integral se convierte en:

I \cong \frac{b-a}{2}(f(x_a) + f(x_b))

cuya fórmula es semejante a una mejor aproximación de un trapecio, cuyos promedios de alturas son puntos internos de [a,b], concepto mostrado en la gráfica.

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Ejercicio

Para el ejercicio y comparación de resultado con los otros métodos, se realiza el cálculo para un tramo en el intervalo [a,b].

\int_1^3 \sqrt{x} \sin(x) dx

x_a = \frac{3+1}{2} + \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}}\Big)= 1.4226

x_b = \frac{3+1}{2} + \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}} \Big) = 2.5773

f(1.4226) = \sqrt{1.4226} \sin(1.4226) = 1.1796

f(2.5773) = \sqrt{2.5773} \sin(2.5773) = 0.8585

con lo que el resultado aproximado del integral se convierte en:

I \cong \frac{3-1}{2}(1.1796 + 0.8585) = 2.0382

que usando instrucciones de Python para obtener los valores:

>>> import numpy as np
>>> (3+1)/2-(3-1)/2*(1/np.sqrt(3))
1.4226497308103743
>>> (3+1)/2+(3-1)/2*(1/np.sqrt(3))
2.5773502691896257
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> fx(1.4226)
1.1796544827404145
>>> fx(2.5773)
0.8585957175067221
>>> (3-1)*(fx(1.4226)+fx(2.5773))/2
2.0382

el resultado se puede mejorar aumentando el número de tramos en el intervalo [a,b]. Por ejemplo, el resultado usando 4 tramos el resultado es semejante al usar el método del trapecio con 128 tramos, lo que muestra el ahorro en cálculos entre los métodos

Integral:  2.05357719003
>>>

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Algoritmo con Python

Instrucciones usando la cuadratura de Gauss como una función

# Integración: Cuadratura de Gauss de dos puntos
# modelo con varios tramos entre [a,b]
import numpy as np
import matplotlib.pyplot as plt

# cuadratura de Gauss de dos puntos
def integraCuadGauss2p(funcionx,a,b):
    x0 = -1/np.sqrt(3)
    x1 = -x0
    xa = (b+a)/2 + (b-a)/2*(x0)
    xb = (b+a)/2 + (b-a)/2*(x1)
    area = ((b-a)/2)*(funcionx(xa) + funcionx(xb))
    return(area)

# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)

# intervalo de integración
a = 1
b = 3
tramos = 4

# PROCEDIMIENTO
muestras = tramos+1
xi = np.linspace(a,b,muestras)
area = 0
for i in range(0,muestras-1,1):
    deltaA = integraCuadGauss2p(fx,xi[i],xi[i+1])
    area = area + deltaA
# SALIDA
print('Integral: ', area)

Gráfica por tramos

La gráfica que complementa el resultado anterior, se realiza añadiendo las instrucciones presentadas a continuación.

Considere que la gráfica es útil con pocos tramos en el intervalo[a,b]

# GRAFICAR por cada Segmento
# para concepto con pocos segmentos
x0 = -1/np.sqrt(3) 
x1 = 1/np.sqrt(3)

# arregos para gráficas
xi = np.array([])
fi = np.array([])

xat = np.array([])
xbt = np.array([])

recta = np.array([])

muestrastramo = 10
subtramo = np.linspace(a,b,muestras)

for i in range(0,tramos,1):
    at = subtramo[i]
    bt = subtramo[i+1]
    
    xit = np.linspace(at,bt,muestrastramo)
    fit = fx(xit)
    
    xi = np.concatenate((xi,xit))
    fi = np.concatenate((fi,fit))

    # puntos xa y xb por tramo
    xa = (bt+at)/2 + (bt-at)/2*(x0)
    xb = (bt+at)/2 + (bt-at)/2*(x1)
    
    xat = np.concatenate((xat,[xa]))
    xbt = np.concatenate((xbt,[xb]))
    
    # Recta entre puntos x0 y x1 por tramo
    m = (fx(xb)-fx(xa))/(xb-xa)
    b0 = fx(xa)- m*xa
    linea = b0 + m*xit
    recta = np.concatenate((recta,linea))

# Marcadores 'o' de xa y xb por tramos
puntox = np.concatenate((xat,xbt))
puntoy = fx(puntox)

# Graficando
# Trazado de lineas
plt.plot(xi,recta, label = 'grado 1', color = 'tab:orange')
plt.fill_between(xi,0,recta, color='tab:olive')
plt.plot(xi,fi, label='f(x)', color = 'blue')

# Verticales para dividir los tramos
for j in range(0,len(subtramo),1):
    plt.axvline(subtramo[j], color='tab:gray')
    
# Marcadores de puntos xa y xb por tramos
for j in range(0,len(xat),1):
    plt.axvline(xat[j], color='w')
    plt.axvline(xbt[j], color='w')
    
plt.plot(puntox,puntoy, 'o', color='g')

plt.title('Integral: Cuadratura Gauss')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()

plt.show()

[ Cuadratura de Gauss ] [ Ejercicio ] [Algoritmo/función Python]

Referencia: Tabla 22.1 Chapra p661

I \cong c_0 f(x_0) + c_1f(x_1) + … + c_{n-1}f(x_{n-1})

Factores usados en las fórmulas de Gauss-Legendre.
Puntos	Factor de ponderación	Argumentos de la función	Error de truncamiento
2	c0 = 1.0000000 c1 = 1.0000000	x0 = – 0.577350269 x1 = 0.577350269	≅ f⁽⁴⁾⁽x )
3	c0 = 0.5555556 c1 = 0.8888889 c2 = 0.5555556	x0 = – 0.774596669 x1 = 0.0 x2 = 0.774596669	≅ f⁽⁶⁾(x )
4	c0 = 0.3478548 c1 = 0.6521452 c2 = 0.6521452 c3 = 0.3478548	x0 = – 0.861136312 x1 = – 0.339981044 x2 = 0.339981044 x3 = 0.861136312	≅f (8)(x )

2017-10-052024-08-11

5.3 Regla de Simpson 3/8

Referencia: Chapra 21.2.1 p.631 pdf.655, Burden 4.2 p192 pdf202, Rodriguez 7.1.8 p288

[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]

Regla de Simpson 3/8

Es el resultado cuando para el integral se utiliza el resultado de una interpolación con polinomio de tercer grado.

I = \int_a^b f(x) \delta x

I \cong \int_a^b f_3 (x) \delta x

Al desarrollar la fórmula de la Regla de Simpson de 3/8 para un segmento con tres tramos con distancia h:

I\cong \frac{3h}{8}[f(x_0)+3f(x_1) +3 f(x_2)+f(x_3)]

siendo el tramo de un segmento [a,b]

h=\frac{b-a}{3}

Error de Truncamiento

error_{truncamiento} = -\frac{3}{80} h^5 f^{(4)} (z)

donde z se encuentra entre [a,b]

[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]

Ejercicio

Para el ejercicio planteado usando seis tramos

f(x)= \sqrt {(x)} \sin(x)

1 \leq x \leq 3

tramos = 6

h = \frac{3-1}{6} = \frac{1}{3}

las muestras para el ejercicio son:

>>> import numpy as np
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> xi = [1, 1+1/3, 1+2/3, 2, 1+4/3, 1+5/3, 3]
>>> fx(xi)
array([0.84147098, 1.12229722, 1.28506615, 1.28594075,
       1.10453193, 0.74672307, 0.24442702]

I\cong \frac{3}{8}\Big(\frac{1}{3}\Big)[f(1)+3f\Big(1+\frac{1}{3}\Big) +3f\Big(1+\frac{2}{3}\Big) + f(2)] +

+ \frac{3}{8}\Big(\frac{1}{3}\Big)[f(2)+3f\Big(2+\frac{1}{3}\Big) +3f\Big(2+\frac{2}{3}\Big)+ f(3)]

f(1)= \sqrt {(1)} \sin(1) = 0.8414

f(4/3)= \sqrt {(4/3)} \sin(4/3) = 1.1222

f(5/3)= \sqrt {(5/3)} \sin(5/3) = 1.2850

f(2)= \sqrt {(2)} \sin(2) = 1.2859

f(7/3)= \sqrt {(7/3)} \sin(7/3) = 1.1045

f(8/3)= \sqrt {(8/3)} \sin(8/3) = 0.7467

f(3)= \sqrt {(3)} \sin(3) = 0.2444

I\cong \frac{3}{24}[0.8414+3(1.1222)+3(1.2850)+1.2859]

+ \frac{3}{24}[1.2859+3(1.1045)+3(0.7467)+0.2444]

I\cong 2.0542

[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]

Algoritmo en Python

A partir del algoritmo para Simpson de 1/3, se realizan modificaciones para obtener el algoritmo de Simpson de 3/8:

Resultados de algoritmo

tramos:  6
Integral con Simpson 3/8:  2.0542043270535757

Caso: f(x) es una expresión matemática

# Integración Simpson 3/8
import numpy as np
import matplotlib.pyplot as plt

def integrasimpson38(fx,a,b,tramos):
    ''' integral con método de Simpson 3/8
        tramos debe ser múltiplo de 3
    '''
    # Validar cantidad de tramos múltiplo de 3
    esmult3 = tramos%3
    if esmult3 != 0:
        suma = 'tramos debe ser múltiplo de 3'
    # Regla de Simpson 3/8
    if esmult3 == 0:
        h = (b-a)/tramos
        xi = a
        suma = 0
        for i in range(0,tramos,3):
            unS38 = (3/8)*h*(fx(xi)+3*fx(xi+h)+3*fx(xi+2*h)+fx(xi+3*h))
            suma = suma + unS38
            xi = xi + 3*h
    return(suma)

# PROGRAMA -----------------
# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)

# intervalo de integración
a = 1
b = 3
tramos = 6

# PROCEDIMIENTO
Area = integrasimpson38(fx,a,b,tramos)

# SALIDA
print('tramos: ',tramos)
print('Integral con Simpson 3/8: ',Area)
if type(Area)==str:
    print('  Revisar errores...')

Caso: x[i], f[i] son muestras

xi = [1.        , 1.33333333, 1.66666667, 2.        ,
      2.33333333, 2.66666667, 3.        ]
fi = [0.84147098, 1.12229722, 1.28506615, 1.28594075,
      1.10453193, 0.74672307, 0.24442702]
tolera = 1e-7

Instrucciones en Python

# Integración Simpson 1/3
# Usando una muestras xi,fi
import numpy as np
import matplotlib.pyplot as plt

def integrasimpson38_fi(xi,fi,tolera = 1e-10):
    ''' sobre muestras de fi para cada xi
        integral con método de Simpson 3/8
        respuesta es np.nan para tramos desiguales,
        no hay suficientes puntos.
    '''
    n = len(xi)
    i = 0
    suma = 0
    while not(i>=(n-3)):
        h  = xi[i+1]-xi[i]
        h1 = (xi[i+2]-xi[i+1])
        h2 = (xi[i+3]-xi[i+2])
        dh = abs(h-h1)+abs(h-h2)
        if dh<tolera:# tramos iguales
            unS38 = fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]
            unS38 = (3/8)*h*unS38
            suma = suma + unS38
        else:  # tramos desiguales
            suma = 'tramos desiguales'
        i = i + 3
    if (i+1)<n: # incompleto, tramos por calcular
        suma = 'tramos incompletos, faltan '
        suma = suma +str(n-(i+1))+' tramos'
    return(suma)

# PROGRAMA -----------------
# INGRESO
xi = [1.        , 1.33333333, 1.66666667, 2.        ,
      2.33333333, 2.66666667, 3.        ]
fi = [0.84147098, 1.12229722, 1.28506615, 1.28594075,
      1.10453193, 0.74672307, 0.24442702]
tolera = 1e-7

# PROCEDIMIENTO
n = len(xi)-1
Area = integrasimpson38_fi(xi,fi,tolera)

# SALIDA
print('tramos: ',n)
print('Integral con Simpson 3/8: ',Area)
if type(Area)==str:
    print('  Revisar errores')

[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo /función Python]

2017-10-052024-08-11

5.2 Regla de Simpson 1/3

Referencia: Chapra 21.2.1 p631 pdf655, Burden 4.2 p192 pdf202, Rodriguez 7.1.4 p281

[ Simpson 1/3 ] [ Ejercicio ] [Algoritmo Python] [ función Python]

La regla de Simpson 1/3

es el resultado cuando se realiza una interpolación con polinomio de segundo grado.

I = \int_a^b f(x) \delta x \cong \int_a^b f_2 (x) \delta x

Usando un polinomio de Lagrange de segundo grado:

I = \int_{x_0}^{x_2} \bigg[ \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} f(x_0) +

+ \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} f(x_1) +

+ \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} f(x_2) \bigg] \delta x

que tiene como resultado para un solo tramo:

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)]

siendo

h=\frac{b-a}{2}

Error de truncamiento

la cota del error de truncamiento se estima como O(h⁵)

error_{trunca} = -\frac{h^5}{90} f^{(4)}(z)

para un valor de z entre [a,b]

para cuantificar el valor, se puede usar la diferencia finita Δ⁴f, pues con la derivada sería muy laborioso.

[ Simpson 1/3 ] [ Ejercicio ] [Algoritmo Python] [ función Python]

Ejercicio

Para el ejercicio planteado en la regla de trapecio, usando cuatro tramos, se aplica el método cada dos tramos.

f(x)= \sqrt {(x)} \sin(x)

1 \leq x \leq 3

tramos = 4

h = \frac{3-1}{4} = \frac{1}{2}

>>> import numpy as np
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> xi = [1, 1+1/2, 1+2/2, 1+3/2,3]
>>> fx(xi)
array([0.84147098, 1.22167687, 1.28594075, 
       0.94626755, 0.24442702])

I\cong \frac{0.5}{3}[f(1)+4f(1.5) + f(2)] +

+ \frac{0.5}{3}[f(2)+4f(2.5) + f(3)]

f(1)= \sqrt {(1)} \sin(1) = 0.8414

f(1.5)= \sqrt {(1.5)} \sin(1.5) = 1.2216

f(2)= \sqrt {(2)} \sin(2) = 1.2859

f(2.5)= \sqrt {(2.5)} \sin(2.5) = 0.9462

f(3)= \sqrt {(3)} \sin(3) = 0.2444

I\cong \frac{0.5}{3}[0.8414+4(1.2216) + 1.2859] +

+ \frac{0.5}{3}[1.2859+4(0.9462) + 0.2444]

I\cong 2.054

Note que al usar Simpson 1/3 con 4 tramos el resultado tiene los 2 primeros decimales iguales a usar Trapecio con 16 tramos.

tramos: 4
Integral:  2.0549261957703937
>>>

[ Simpson 1/3 ] [ Ejercicio ] [Algoritmo Python] [ función Python]
..

Algoritmo en Python

Del ejercicio con trapecios, se repite el ejercicio con n tramos; usando dos tramos (tres puntos) en cada iteración.
Cada iteración se procesa avanzando dos puntos x_i, x_i+h, x_i+2h . Ejemplo:

tramos:  8
Integral:  2.053709383061734
>>>

Instrucciones en Python

Se realiza mediante la aplicación directa de la fórmula para cada segmento conformado de dos tramos. Se verifica que el valor de tramos sea par.

# Integración: Regla Simpson 1/3
import numpy as np
import matplotlib.pyplot as plt

# INGRESO:
fx = lambda x: np.sqrt(x)*np.sin(x)

# intervalo de integración
a = 1
b = 3
tramos = 8

# Validar cantidad de tramos pares
esimpar = tramos%2
while (esimpar == 1):
    print('tramos: ',tramos)
    tramos = int(input('tramos debe ser par: '))
    esimpar = tramos%2

# PROCEDIMIENTO
# Regla de Simpson 1/3
h = (b-a)/tramos
xi = a
area = 0
for i in range(0,tramos,2):
    deltaA = (h/3)*(fx(xi)+4*fx(xi+h)+fx(xi+2*h))
    area = area + deltaA
    xi = xi + 2*h

# SALIDA
print('tramos:', tramos)
print('Integral: ', area)

Gráfica

Se puede observar mejor lo expresado usando la gráfica para observar los tramos, muestras, por segmento.

Instrucciones en Python adicionales al algoritmo anterior

# GRAFICA
# fx suave aumentando muestras
muestrasfxSuave = 4*tramos + 1
xk = np.linspace(a,b,muestrasfxSuave)
fk = fx(xk)
#plt.fill_between(xj,0,fj, color='g')
plt.plot(xk,fk, label='f(x)')

# fx muestras por tramo
muestras = tramos + 1
xi = np.linspace(a,b,muestras)
fi = fx(xi)
fi0 = np.zeros(muestras) # linea base
plt.plot(xi,fi,'o', label='f(xi)')
for i in range(0,muestras,1):
    plt.vlines(xi,fi0,fi,linestyle='dotted')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f')
plt.legend()
plt.show()

[ Simpson 1/3 ] [ Ejercicio ] [Algoritmo Python] [ función Python]
..

Algoritmo como función de Python

Caso: f(x) es una expresión matemática

A partir del ejercicio anterior, se resume en una función de Python si la entrada f(x) es una expresión matemática:

def integrasimpson13(fx,a,b,tramos):
    ''' integral con método de Simpson 1/3
        tramos debe debe ser múltiplo de 2
    '''
    # Validar cantidad de tramos pares
    esmult2 = tramos%2
    if esmult2 != 0:
        suma = 'tramos debe ser múltiplo de 2'
    # Regla de Simpson 1/3
    if esmult2 == 0:
        h = (b-a)/tramos
        xi = a
        suma = 0
        for i in range(0,tramos,2):
            unS13 = (h/3)*(fx(xi)+4*fx(xi+h)+fx(xi+2*h))
            suma = suma + unS13
            xi = xi + 2*h
    return(suma)

Caso: x[i], f[i] son muestras

xi = [1. , 1.5, 2. , 2.5, 3.]
fi = [0.84147098, 1.22167687, 1.28594075,
      0.94626755, 0.24442702]

Cuando se integra sobre muestras dadas por los vectores xi, fi. Se revisa que los tramos entre muestras sean iguales para un Simpson 1/3 y que existan suficientes puntos para completar el integral.

# Integración Simpson 1/3
# Usando una muestras xi,fi
import numpy as np
import matplotlib.pyplot as plt

def integrasimpson13_fi(xi,fi,tolera = 1e-10):
    ''' sobre muestras de fi para cada xi
        integral con método de Simpson 1/3
        respuesta es np.nan para tramos desiguales,
        no hay suficientes puntos.
    '''
    n = len(xi)
    i = 0
    suma = 0
    while not(i>=(n-2)):
        h = xi[i+1]-xi[i]
        dh = abs(h - (xi[i+2]-xi[i+1]))
        if dh<tolera:# tramos iguales
            unS13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2])
            suma = suma + unS13
        else:  # tramos desiguales
            suma = 'tramos desiguales'
        i = i + 2
    if i<(n-1): # incompleto, faltan tramos por calcular
        suma = 'tramos incompletos, faltan '
        suma = suma ++str((n-1)-i)+' tramos'
    return(suma)

# PROGRAMA -----------------
# INGRESO
xi = [1. , 1.5, 2. , 2.5, 3.]
fi = [0.84147098, 1.22167687, 1.28594075,
      0.94626755, 0.24442702]
# PROCEDIMIENTO
Area = integrasimpson13_fi(xi,fi)

# SALIDA
print('tramos: ',len(xi)-1)
print('Integral con Simpson 1/3: ',Area)
if type(Area)==str:
    print('  Revisar errores...')

resultados

tramos:  4
Integral con Simpson 1/3:  2.0549261966666665
>>>

[ Simpson 1/3 ] [ Ejercicio ] [Algoritmo Python] [ función Python]

Fórmula con varios segmentos y h constante

Usado cuando el intervalo a integrar tiene varios segmentos, cada segmento tiene dos tramos. Ejemplo para dos segmentos, cuatro tramos, semejante al usado en la gráfica. La simplificación es válida si h es constante.

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)] +

+ \frac{h}{3}[f(x_2)+4f(x_3) + f(x_4)]

tomando factor común h/3

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + 2f(x_2) +

+4f(x_3) + f(x_4)]

2017-10-052024-08-09

5.1 Regla del Trapecio para Integración numérica con Python

Referencia: Chapra 21.1 p621 pdf645, Burden 4.2 p192 pdf202, Rodríguez 7.1.1 p27

[ Regla del trapecio ] [ Ejercicio ] [Algoritmo Python] [ función Python]

Regla del Trapecio

La integración numérica con la regla del trapecio usa un polinomio de primer grado como aproximación de f(x) entre los extremos a y b del intervalo.

Es la primera de las formulas cerradas de Newton-Cotes.

I = \int_a^b f(x) dx \cong \int_a^b f_1 (x) dx

usando el rango entre [a,b] el polinomio se aproxima con una línea recta:

f_1 (x) = f(a) + \frac{f(b)-f(a)}{b-a} (x-a)

el área bajo esta línea recta es una aproximación de la integral de f(x) entre los límites a y b.

El resultado del integral es la regla del trapecio:

I = (b-a) \frac{f(a)+f(b)}{2}

que se interpreta como la multiplicación entre la base y altura promedio de un trapecio. También se llega al resultando sumando las áreas de sus componentes: rectángulo y triángulo.

El error de truncamiento se encuentra como el integral del término que le sigue al polinomio de Taylor en la aproximación, es decir el de grado 2, que al integrarlo tiene un orden de h³. (Rodríguez p275)

error_{truncar} = -\frac{h^3}{12}f''(z)

a < z < b

[ Regla del trapecio ] [ Ejercicio ] [Algoritmo Python] [ función Python]

Ejemplo de Integración con el método del trapecio

Para integrar la función en el intervalo [1,3] con 4, 16, 32 ,64 y 128 tramos,

f(x)= \sqrt {(x)} \sin(x)

Tramos = 4

La base de los trapecios (x_i-x_i+1), si esta base tiene valores equidistantes se sustituye por la variable h .

base =\frac{b-a}{tramos}=\frac{3-1}{4}= 0.5 = h

para cada tramo, el área de un trapecio es:

A_i = base\frac{f(x_i)+f(x_{i+1})}{2}

por lo que cada trapecio en cada subintervalo tendrá un área de:

A_1 = (0.5)\frac{f(1)+f(1.5)}{2}

A_2 = (0.5)\frac{f(1.5)+f(2)}{2}

A_3 = (0.5)\frac{f(2)+f(2.5)}{2}

A_4 = (0.5)\frac{f(2.5)+f(3)}{2}

y el integral de todo el intervalo es la suma de todos los trapecios.

Integral = A_1+ A_2+ A_3+A_4

si se quiere tomar el factor común entre las sumas de áreas de cada tramo, también se tiene la forma de la ecuación con un h equidistante entre cada tramo del intervalo.

Integral = \frac{0.5}{2}\Big(f(1)+2f(1.5) +2f(2)+2f(2.5)+f(3)\Big)

Interpretando la fórmula, el integral es la suma de:

una vez la función evaluada en cada extremo,
mas dos veces cada valor de la función evaluada en los puntos intermedios.
El resultado de la suma se multiplica por h/2.

En caso que los puntos no sean equidistantes la simplificación NO procede, y se sumaran las áreas de los trapecios de cada tramo.

Siguiendo el procedimiento, para cada cantidad de tramos en el intervalo, los resultados serán:

tramos: 4
Integral: 1.99841708623

tramos:  16
Integral:  2.05019783717

tramos:  32
Integral:  2.05277225085

tramos:  64
Integral:  2.05341563776

tramos: 128
Integral:  2.05357647096

[ Regla del trapecio ] [ Ejercicio ] [Algoritmo Python] [ función Python]

Algoritmo en Python – Regla o Método del trapecio

Algoritmo con fórmula simplificada para varios tramos, con puntos de muestras equidistantes h.

# Integración: Regla de los trapecios
# Usando una función fx()
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)

# intervalo de integración
a = 1
b = 3
tramos = 4

# PROCEDIMIENTO
# Regla del Trapecio
# Usando tramos equidistantes en intervalo
h = (b-a)/tramos
xi = a
suma = fx(xi)
for i in range(0,tramos-1,1):
    xi = xi + h
    suma = suma + 2*fx(xi)
suma = suma + fx(b)
area = h*(suma/2)

# SALIDA
print('tramos: ', tramos)
print('Integral: ', area)

La gráfica como ayuda didáctica, si la cantidad de tramos sea «poca», muestra los trapecios, si aumenta la cantidad de tramos, no es necesario poner líneas verticales en blanco para separar los trapecios:

# GRAFICA
# Puntos de muestra
muestras = tramos + 1
xi = np.linspace(a,b,muestras)
fi = fx(xi)
# Linea suave
muestraslinea = tramos*10 + 1
xk = np.linspace(a,b,muestraslinea)
fk = fx(xk)

# Graficando
plt.plot(xk,fk, label ='f(x)')
plt.plot(xi,fi, marker='o',
         color='orange', label ='muestras')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Integral: Regla de Trapecios')
plt.legend()

# Trapecios
plt.fill_between(xi,0,fi, color='g')
for i in range(0,muestras,1):
    plt.axvline(xi[i], color='w')

plt.show()

Para rellenar el área bajo la curva se usa la instrucción plt.fill_between(xi,0,fi, color=’g’). La división de los trapecios con una línea blanca (white) se realiza con la instrucción plt.axvline(xi[i], color=’w’).

[ Regla del trapecio ] [ Ejercicio ] [Algoritmo Python] [ función Python]

Algoritmo como función de Python

Caso: f(x) es una expresión matemática

A partir del ejercicio anterior, se resume en una función de Python si la entrada f(x) es una expresión matemática:

def integratrapecio(funcionx,a,b,tramos):
    h = (b-a)/tramos
    xi = a
    suma = fx(xi)
    for i in range(0,tramos-1,1):
        xi = xi + h
        suma = suma + 2*fx(xi)
    suma = suma + fx(b)
    area = h*(suma/2)
    return(area)

Caso: x[i], f[i] son muestras

Algoritmo usando las muestras y para tramos que pueden tener distancias arbitrarias. En este caso se usa la formula del área del trapecio para cada tramo.

Usado para ejercicios donde los datos proporcionados son muestras. Se adapta el bloque de ingreso y el procedimiento inicia desde «Regla de Trapecio». La cantidad de tramos será el numero de muestras menos uno tramos = len(xi) - 1

# Integración: Regla de los trapecios
# Usando una muestras xi,fi
import numpy as np
import matplotlib.pyplot as plt

def integratrapecio_fi(xi,fi):
    ''' sobre muestras de fi para cada xi
        integral con método de trapecio
    '''
    n = len(xi)
    suma = 0
    for i in range(0,n-1,1):
        dx = xi[i+1]-xi[i]
        untrapecio = dx*(fi[i+1]+fi[i])/2
        suma = suma + untrapecio
    return(suma)

# PROGRAMA -----------------
# INGRESO
xi = [1. , 1.5, 2. , 2.5, 3. ]
fi = [0.84147098, 1.22167687, 1.28594075,
      0.94626755, 0.24442702]

# PROCEDIMIENTO
Area = integratrapecio_fi(xi,fi)

# SALIDA
print('tramos: ',len(xi)-1)
print('Integral con trapecio: ',Area)

[ Regla del trapecio ] [ Ejercicio ] [Algoritmo Python] [ función Python]