Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta d2y/dx2 ]
..
1. Ejercicio
Referencia: Chapra 28.2 p831 pdf855, Rodriguez 9.2.1 p263
https://es.wikipedia.org/wiki/Ecuaciones_Lotka%E2%80%93Volterra
https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations
Modelos depredador-presa y caos. Ecuaciones Lotka-Volterra. En el sistema de ecuaciones:
\frac{dx}{dt} = ax - bxy \frac{dy}{dt} = -cy + dxy variables
variables
x = número de presas
y = número de depredadores
t = tiempo de observación
coeficientes
a = razón de crecimiento de la presa, (0.5)
c = razón de muerte del depredador (0.35)
b = efecto de la interacción depredador-presa sobre la muerte de la presa (0.7)
d = efecto de la interacción depredador-presa sobre el crecimiento del depredador, (0.35)
Considere como puntos iniciales en la observación de las especies:
t = 0, x = 2, y = 1, h = 0.5
Los términos que multiplican xy hacen que las ecuaciones sean no lineales.
Observe que la variable tiempo no se encuentra en las expresiones f y g, h se aplica a tiempo.
Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta d2y/dx2 ]
..
2. Desarrollo analítico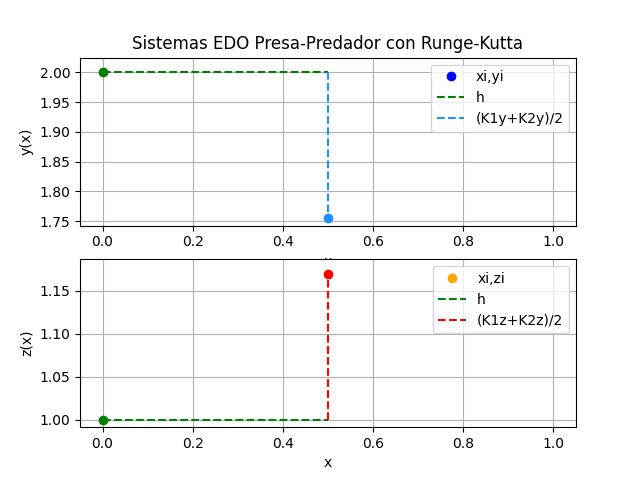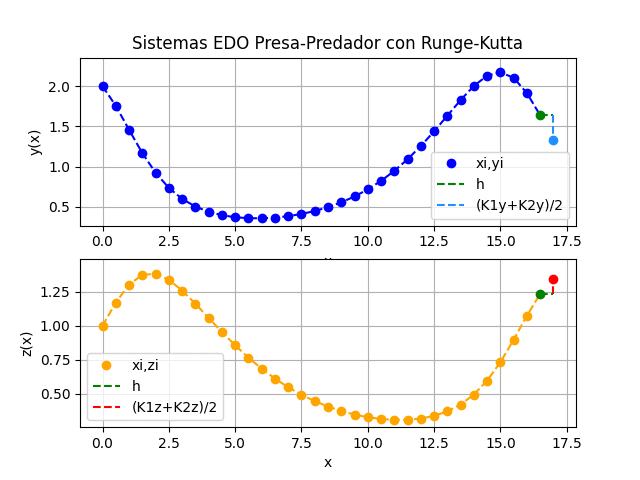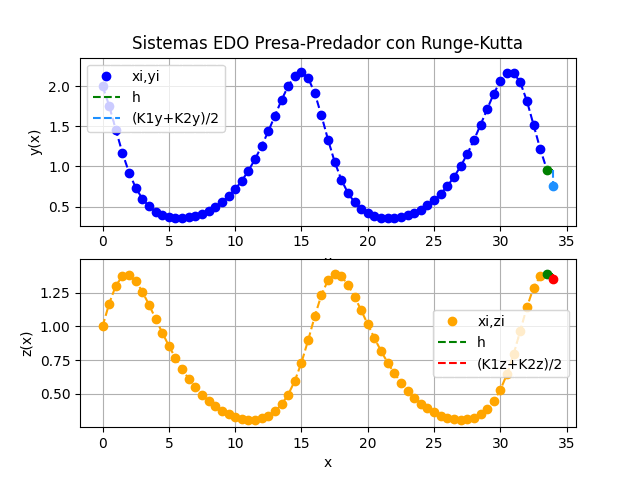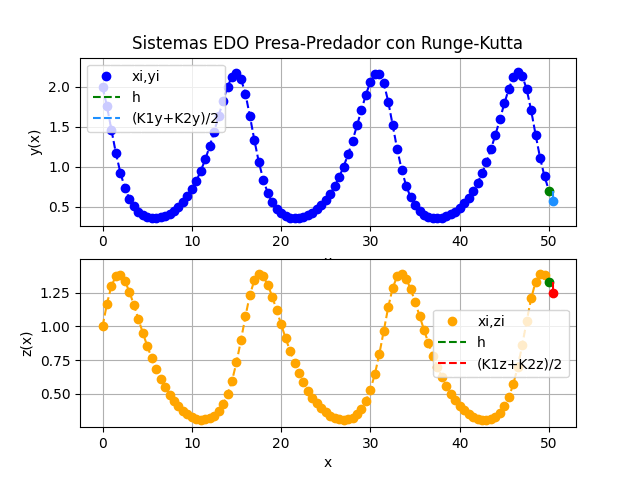
Para resolver el sistema, se plantean las ecuaciones de forma simplificada para el algoritmo:
f(t,x,y) = 0.5 x - 0.7 xy g(t,x,y) = -0.35y + 0.35xyLas expresiones se adaptan al método de Runge-Kutta para primeras derivadas por cada variable de población. Se deben usar de forma simultánea para cada tiempo t.
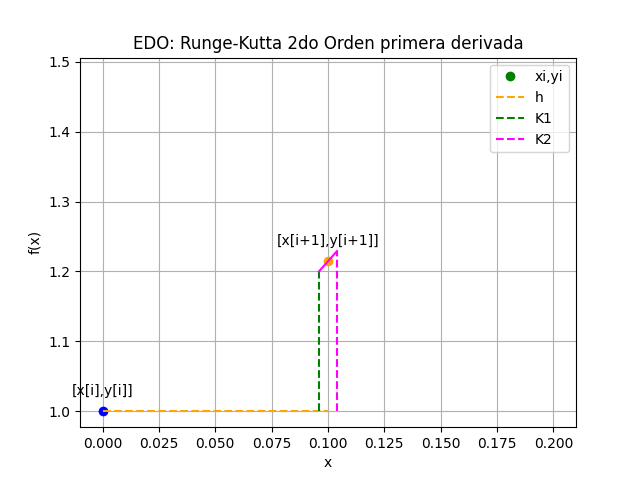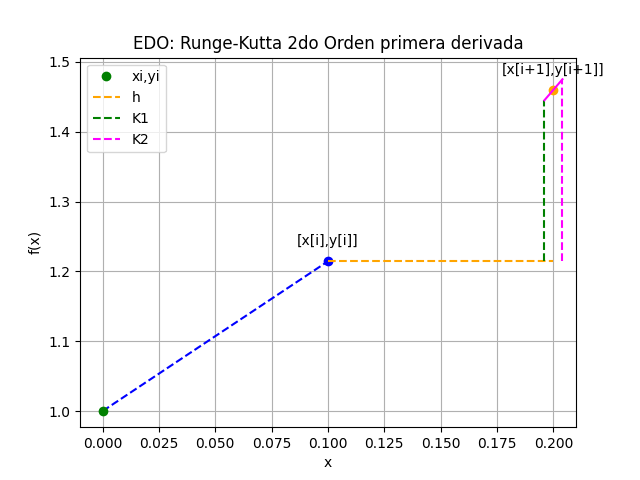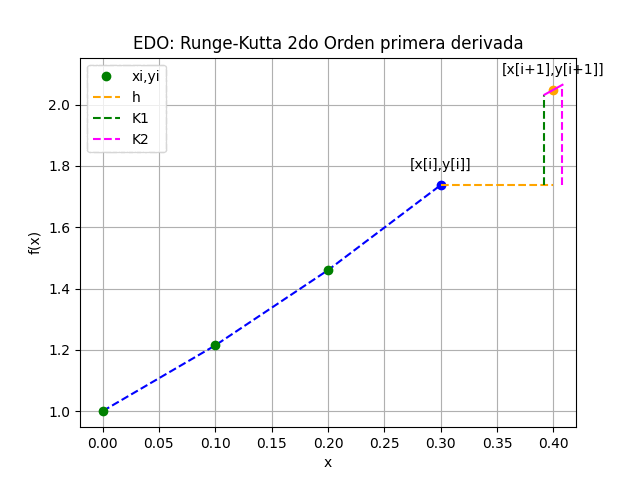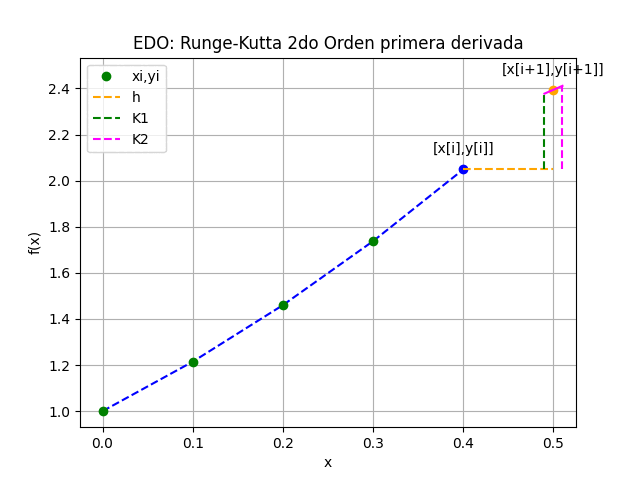
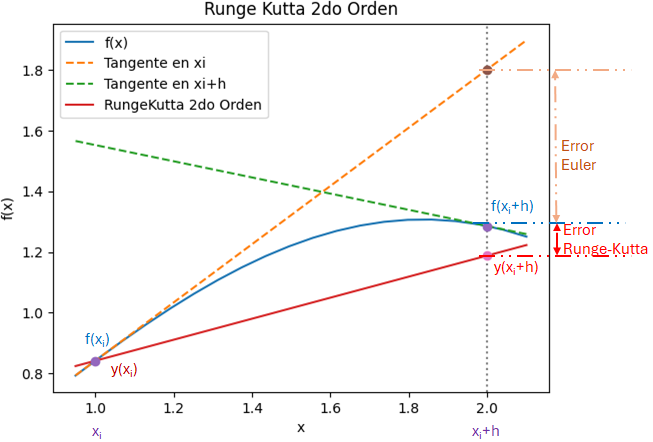
K1x = h f(t,x,y) = 0.5 \Big( 0.5 x - 0.7 xy \Big) K1y = h g(t,x,y) = 0.5 \Big(-0.35y + 0.35xy \Big)..
K2x = h f(t+h,x+K1x,y+K1y) = 0.5 \Big( 0.5 (x+K1x) - 0.7 (x+K1x)(y+K1y) \Big) K2y = h g(t+h,x+K1x,y+K1y) = 0.5 \Big(-0.35(y+K1y) + 0.35(x+K1x)(y+K1y) \Big)..
x[i+1] = x[i] + \frac{K1x+K2x}{2} y[i+1] = y[i] + \frac{K1y+K2y}{2} t[i+1] = t[i] + hcon lo que se puede aplicar al ejercicio en cada iteración. dadas las condiciones iniciales.
Itera = 0
t = 0, x = 2, y = 1, h = 0.5
K1x = 0.5 f(0,2,1) = 0.5 \Big( 0.5 (2) - 0.7 (2)(1) \Big) = -0.2 K1y = 0.5 g(0,2,1) = 0.5 \Big(-0.35(1) + 0.35(2)(1) \Big) =0.175..
K2x = 0.5 f(0+0.5, 2+(-0.2), 1+0.175) = 0.5 \Big( 0.5 (2+(-0.2)) - 0.7 (2+(-0.2))(1+0.175) \Big) = -0.29025 K2y = 0.5 g(0+0.5, 2+(-0.2), 1+0.175) = 0.5 \Big(-0.35(1+0.175) + 0.35(2+(-0.2))(1+0.175) \Big) = 0.1645..
x[1] = x[0] + \frac{K1x+K2x}{2} = 2 + \frac{-0.2+(-0.29025)}{2} = 1.7548 y[1] = y[0] + \frac{K1y+K2y}{2} = 1 + \frac{0.175+0.1645}{2}= 1.1697 t[1] = t[0] + h = 0 +0.5 = 0.5itera = 1
t = 0.5, x = 1.7548, y = 1.1697, h = 0.5
K1x = 0.5 \Big( 0.5 (0,1.7548) - 0.7 (0,1.7548)(1.1697) \Big) = -0.2797 K1y = 0.5 \Big(-0.35(1.1697) + 0.35(1.7548)(1.1697) \Big) =0.1545..
K2x = 0.5 \Big( 0.5 (1.7548+(-0.2797)) - 0.7 (1.7548+(-0.2797))(1.1697+0.1545) \Big) =-0.3149 K2y = 0.5 \Big(-0.35(1.1697+0.1545) + 0.35(1.7548+(-0.2797))(1.1697+0.1545) \Big) = 0.1645..
x[2] = 1.7548 + \frac{-0.2797+(-0.3149)}{2} = 1.4575 y[2] = 1.1697 + \frac{0.1545+0.1645}{2} = 1.3020 t[2] = t[0] + h = 0.5 +0.5 = 1itera=2
t = 1, x = 1.4575, y = 1.3020, h = 0.5
continuar como tarea …
Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta d2y/dx2 ]
3. Algoritmo en Python
Planteamiento que se ingresan al algoritmo con el algoritmo rungekutta2_fg(fx,gx,x0,y0,z0,h,muestras), propuesto en
Al ejecutar el algoritmo se obtienen los siguientes resultados:
Runge-Kutta Segunda derivada i [ xi, yi, zi ] [ K1y, K1z, K2y, K2z ] 0 [0. 2. 1.] [0. 0. 0. 0.] 1 [0.5 1.754875 1.16975 ] [-0.2 0.175 -0.29025 0.1645 ] 2 [1. 1.457533 1.302069] [-0.279749 0.154528 -0.314935 0.11011 ] 3 [1.5 1.167405 1.373599] [-0.29985 0.104254 -0.280406 0.038807] 4 [2. 0.922773 1.381103] [-0.26939 0.040241 -0.219874 -0.025233] 5 [2.5 0.734853 1.33689 ] [-0.215362 -0.018665 -0.160478 -0.069761] 6 [3. 0.598406 1.258434] [-0.160133 -0.062033 -0.11276 -0.09488 ] ...
Los resultados de la tabla se muestran parcialmente, pues se usaron mas de 100 iteraciones.
Los resultados se pueden observar de diferentes formas:
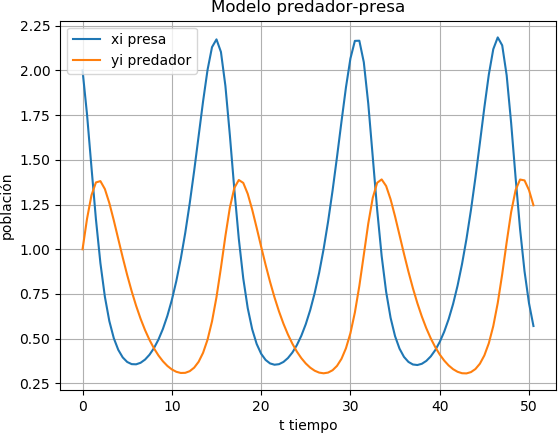
a) Cada variable xi, yi versus ti, es decir cantidad de animales de cada especie durante el tiempo de observación
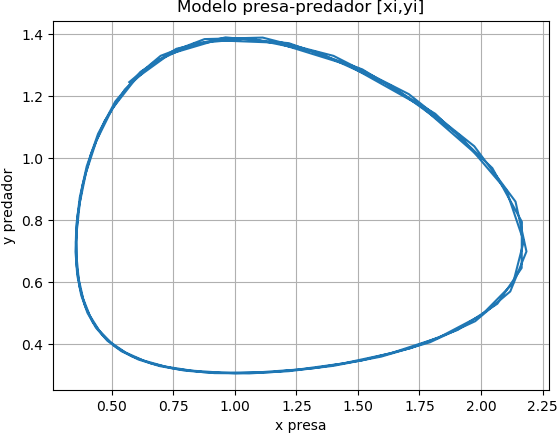
b) Independiente de la unidad de tiempo, xi vs yi, muestra la relación entre la cantidad de presas y predadores. Relación que es cíclica y da la forma a la gráfica.
Las instrucciones del algoritmo en Python usadas en el problema son:
# Modelo predador-presa de Lotka-Volterra # Sistemas EDO con Runge Kutta de 2do Orden import numpy as np def rungekutta2_fg(f,g,x0,y0,z0,h,muestras, vertabla=False, precision = 6): ''' solucion a EDO con Runge-Kutta 2do Orden Segunda derivada, x0,y0 son valores iniciales, h es tamano de paso, muestras es la cantidad de puntos a calcular. ''' tamano = muestras + 1 tabla = np.zeros(shape=(tamano,3+4),dtype=float) # incluye el punto [x0,y0,z0] tabla[0] = [x0,y0,z0,0,0,0,0] xi = x0 yi = y0 zi = z0 i=0 if vertabla==True: print('Runge-Kutta Segunda derivada') print('i ','[ xi, yi, zi',']') print(' [ K1y, K1z, K2y, K2z ]') np.set_printoptions(precision) print(i,tabla[i,0:3]) print(' ',tabla[i,3:]) for i in range(1,tamano,1): K1y = h * f(xi,yi,zi) K1z = h * g(xi,yi,zi) K2y = h * f(xi+h, yi + K1y, zi + K1z) K2z = h * g(xi+h, yi + K1y, zi + K1z) yi = yi + (K1y+K2y)/2 zi = zi + (K1z+K2z)/2 xi = xi + h tabla[i] = [xi,yi,zi,K1y,K1z,K2y,K2z] if vertabla==True: txt = ' ' if i>=10: txt=' ' print(str(i)+'',tabla[i,0:3]) print(txt,tabla[i,3:]) return(tabla) # PROGRAMA ------------------ # INGRESO # Parámetros de las ecuaciones a = 0.5 b = 0.7 c = 0.35 d = 0.35 # Ecuaciones f = lambda t,x,y : a*x -b*x*y g = lambda t,x,y : -c*y + d*x*y # Condiciones iniciales t0 = 0 x0 = 2 y0 = 1 # parámetros del algoritmo h = 0.5 muestras = 101 # PROCEDIMIENTO tabla = rungekutta2_fg(f,g,t0,x0,y0,h,muestras,vertabla=True) ti = tabla[:,0] xi = tabla[:,1] yi = tabla[:,2] # SALIDA print('Sistemas EDO: Modelo presa-predador') ##np.set_printoptions(precision=6) ##print(' [ ti, xi, yi]') ##print(tabla[:,0:4])
Los resultados numéricos se usan para generar las gráficas presentadas, añadiendo las instrucciones:
# GRAFICA tiempos vs población import matplotlib.pyplot as plt fig_t, (graf1,graf2) = plt.subplots(2) fig_t.suptitle('Modelo predador-presa') graf1.plot(ti,xi, color='blue',label='xi presa') #graf1.set_xlabel('t tiempo') graf1.set_ylabel('población x') graf1.legend() graf1.grid() graf2.plot(ti,yi, color='orange',label='yi predador') graf2.set_xlabel('t tiempo') graf2.set_ylabel('población y') graf2.legend() graf2.grid() # gráfica xi vs yi fig_xy, graf3 = plt.subplots() graf3.plot(xi,yi) graf3.set_title('Modelo presa-predador [xi,yi]') graf3.set_xlabel('x presa') graf3.set_ylabel('y predador') graf3.grid() plt.show()
Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta d2y/dx2 ]