Ejercicio: 2Eva_IT2018_T1 Paracaidista wingsuit
La solución se puede proponer de dos formas:
[ a. Planteamiento con 1ra Derivada e Integral ]
[ b. Planteamiento con 2da Derivada usando Runge-Kutta]
a. Planteamiento con 1ra Derivada
El problema para un tiempo de observación t>0, se puede dividir en dos partes: velocidad y altura.
- Determinar velocidad: Se aplica Runge-Kutta con los valores iniciales dados, descartar calcular las alturas.
- Determinar las altura: Con los valores de velocidades y la altura inicial de 1 km = 1000 m puede integrar cada tramo.
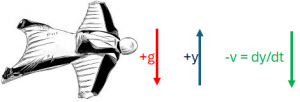
Observe las unidades de medida y que la velocidad es contraria al eje de altura dy/dt = -v. - En el ejercicio se presentan los resultados integrando por trapecios y como otra forma usando la fórmula de Taylor, tomando los puntos encontrados para velocidad.
- Otra opción para las alturas, en caso de requerir determinar el tiempo exacto en que sucede el resultado es sustituir -v = dy/dt y resolver nuevamente la ecuación inicial. (Tarea).
Resultados
La velocidad máxima, si no hubiese límite en la altura, se encuentra en alrededor de 62.39 m/s.
Sin embargo, luego de 20 segundos se observa que la altura alcanza el valor de cero, es decir se alcanzó tierra con velocidad de 62 m/s, que son algo mas de 223 Km/s, el objeto se estrella…!
altura1 con trapecio, altura2 con Taylor [tiempo, velocidad, altura1, altura2] [[ 0. 0. 1000. 1000. ] [ 2. 18.64 981.36 980.4 ] [ 4. 34.04 928.68 925.26] [ 6. 45.02 849.62 843.37] [ 8. 52.13 752.47 743.87] [ 10. 56.49 643.85 633.59] [ 12. 59.07 528.3 516.97] [ 14. 60.58 408.65 396.68] [ 16. 61.45 286.63 274.28] [ 18. 61.94 163.24 150.66] [ 20. 62.23 39.07 26.36] [ 22. 62.39 -85.55 -98.34]]
Los cálculos se realizaron usando las instrucciones en Python:
# 2da Evaluación I Término 2018 # Tema 1. Paracaidista wingsuit import numpy as np def rungekutta2(d1y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,2),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0] xi = x0 yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (K1+K2)/2 xi = xi + h estimado[i] = [xi,yi] return(estimado) def integratrapecio(xi,fi,y0): tamano = len(xi) yi = np.zeros(tamano,dtype = float) yi[0] = y0 for i in range(1,tamano,1): h = xi[i]-xi[i-1] trapecio = h*(fi[i]+fi[i-1])/2 yi[i]= yi[i-1] + trapecio return(yi) # PROGRAMA # INGRESO g = 9.8 cd = 0.225 m = 90 t0 = 0 v0 = 0 dt = 2 y0 = 1000 muestras = 11 d1v = lambda t,v: g - (cd/m)*(v**2) # PROCEDIMIENTO velocidad = rungekutta2(d1v,t0,v0,dt,muestras) ti = velocidad[:,0] vi = velocidad[:,1] # Altura, velocidad es contraria altura, # integrar en cada tramo por trapecios o Cuadratura de Gauss altura = integratrapecio(ti,-vi,y0) # Tabla de resultados altura = np.transpose([altura]) tabla = np.concatenate((velocidad,altura), axis = 1) # otra forma: usando Taylor altura2 = np.zeros(muestras+1,dtype = float) altura2[0] = y0 for i in range(0, muestras,1): acelera = d1v(ti[i],vi[i]) altura2[i+1] = altura2[i] -(vi[i]*dt + acelera*(dt**2)/2) # Tabla de resultados altura2 = np.transpose([altura2]) tabla = np.concatenate((tabla,altura2), axis = 1) # SALIDA np.set_printoptions(precision=2) print('altura1 con trapecio, altura2 con Taylor') print(' [tiempo, velocidad, altura1,altura2]') print(tabla)
y para la gráfica:
# Gráfica import matplotlib.pyplot as plt plt.subplot(211) plt.plot(ti,vi,'g') plt.plot(ti,vi,'bo') plt.title('paracaidista Wingsuit') plt.ylabel('velocidad (m/s)') plt.subplot(212) plt.plot(ti,altura) plt.plot(ti,altura,'o') plt.plot(ti,altura2) plt.axhline(0, color= 'red') plt.ylabel('altura (m)') plt.xlabel('tiempo (s)') plt.show()
b. Planteamiento con 2da Derivada usando Runge-Kutta
La expresión:
\frac{dv}{dt} = g - \frac{cd}{m} v^2se puede plantear como \frac{dy}{dt} = -v
\frac{dy^2}{dt^2} = g - \frac{cd}{m} \Big( \frac{dy}{dt} \Big) ^2Que es una ecuación de 2da derivada y también puede ser resuelta con Runge Kutta para segunda derivada donde:
f(t,y,v) = -v g(t,y,v) = g - \frac{cd}{m} v^2f(t,y,v) = -v g(t,y,v) = 9.8 - \frac{0.225}{90} v^2
con las condiciones iniciales del ejercicio t0 = 0 , y0 = 1000, v0 = 0
En las iteraciones, recuerde que
t se corrige con t+h
y se corrige con y+K1y
v se corrige con v+K1v
itera = 0
K1y = h f(t,y,v) = 2*(0) = 0 K1v = h g(t,y,v) = 2(9.8 - \frac{0.225}{90} 0^2) = 19.6..
K2y = h f(t+h, y+K1y, v + K1v) = 2*(-(0 + 19.6)) = -39.2
..
y_1 = y_0 + \frac{K1y+K2y}{2} = 1000 + \frac{0-39.2}{2}= 980.4
| ti | yi | vi |
| 0 | 1000 | 0 |
| 2 | 980.4 | 18.63 |
| … |
tarea: itera 1 y 2
Instrucciones en Python
# 2Eva_IT2018_T1 Paracaidista wingsuit import numpy as np import matplotlib.pyplot as plt def rungekutta2_fg(f,g,x0,y0,z0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,3),dtype=float) # incluye el punto [x0,y0,z0] estimado[0] = [x0,y0,z0] xi = x0 yi = y0 zi = z0 for i in range(1,tamano,1): K1y = h * f(xi,yi,zi) K1z = h * g(xi,yi,zi) K2y = h * f(xi+h, yi + K1y, zi + K1z) K2z = h * g(xi+h, yi + K1y, zi + K1z) yi = yi + (K1y+K2y)/2 zi = zi + (K1z+K2z)/2 xi = xi + h estimado[i] = [xi,yi,zi] return(estimado) # PROGRAMA PRUEBA # INGRESO f = lambda t,y,v: -v # el signo, revisar diagrama cuerpo libre g = lambda t,y,v: 9.8 - (0.225/90)*(v**2) t0 = 0 y0 = 1000 v0 = 0 h = 2 muestras = 15+1 # PROCEDIMIENTOi tabla = rungekutta2_fg(f,g,t0,y0,v0,h,muestras) ti = tabla[:,0] yi = tabla[:,1] vi = tabla[:,2] # SALIDA print('estimado[ti,yi,vi]') print(tabla) # grafica plt.subplot(211) plt.plot(ti,yi,label='Altura y(t)',) plt.legend() plt.ylabel('velocidad (m/s)') plt.title('paracaidista Wingsuit') plt.subplot(212) plt.plot(ti,vi,label='velocidad v(t)', color='orange') plt.legend() plt.xlabel('tiempo (s)') plt.ylabel('velocidad (m/s)') plt.show()