s1Eva_IIT2007_T1 Distribución binomial acumulada

Ejercicio: 1Eva_IIT2007_T1 Distribución binomial acumulada

Dado F=0.4, dado que n=5 y k=1

Con lo que la fórmula para el objetivo se convierte en:

F = \Bigg( \begin{array}{c} 5 \\ 0 \end{array} \Bigg) p ^0 (1-p)^{(5-0)} + \Bigg( \begin{array}{c} 5 \\ 1 \end{array} \Bigg) p ^1 (1-p)^{(5-1)} = 0.4

para buscar la raíz:

f(p) = (1-p)^{5} + 5p (1-p)^{4} - 0.4

Los valores de las combinatorias se calculan como:

>>> import scipy.special as sts
>>> sts.comb(5,0,repetition=False)
1.0
>>> sts.comb(5,1,repetition=False)
5.0
>>> 

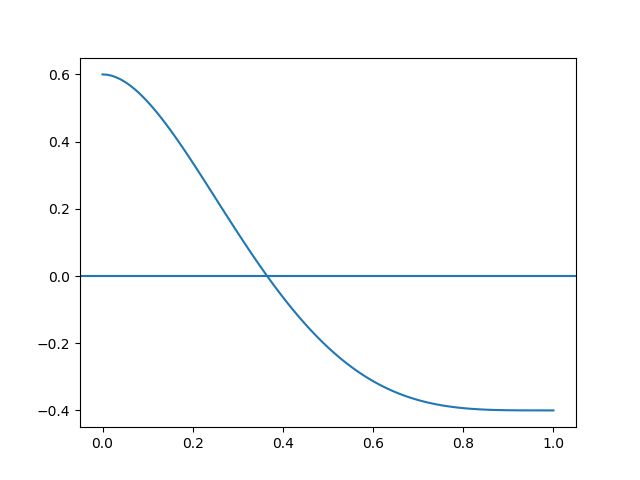
como referencia se revisa la gráfica para f(p)

# 1ra Eval II Término 2007
# Tema 1. Distribución binomial acumulada
import numpy as np
import matplotlib.pyplot as plt
import scipy.special as sts

fp = lambda p: (1-p)**5 + 5*p*((1-p)**4) - 0.4

a = 0
b = 1
pasos = 100

# PROCEDIMIENTO
xi = np.linspace(a,b,pasos+1)
p_i = fp(xi)

# SALIDA
plt.plot(xi,p_i)
plt.axhline(0)
plt.show()

f(p) = (1-p)^5 + 5p(1-p)^4 - 0.4 = (1-p)^4 (1 - p + 5p) - 0.4 = (1-p)^4 (1 + 4p) - 0.4 = (1-p)^2 (1-p)^2 (1 + 4p) - 0.4 = (1-2p+p^2) (1-2p+p^2) (1 + 4p) - 0.4 = (1 - 4p + 6p^2 - 4p^3 +p^4 ) (1 + 4p) - 0.4 = 1 - 10p^2 + 20p^3 + 15p^4 + 4p^5 - 0.4 = 0.6 - 10p^2 + 20p^3 + 15p^4 + 4p^5

y su derivada:

f'(p) = - 20p + 60p^2 + 60p^3 +20p^4
con lo que se puede desarrollar Newton-Raphson…

Verificando el polinomio a usar con python:

>>> import sympy as sp
>>> p = sp.Symbol('p')
>>> poli = (1-p)**5 + 5*p*((1-p)**4) - 0.4
>>> pol = poli.expand()
>>> pol
4*p**5 - 15*p**4 + 20*p**3 - 10*p**2 + 0.6
>>> pol.diff(p,1)
20*p**4 - 60*p**3 + 60*p**2 - 20*p

Tarea: con lo que puede continuar con el procedimiento para encontrar la raiz…

verificar con raiz: 0.3649852264049102

---

Newton-Raphson

# Método de Newton-Raphson
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)
import numpy as np

def newtonraphson(funcionx, fxderiva, c, tolera):
    tramo = abs(2*tolera)
    while (tramo>=tolera):
        xnuevo = c - funcionx(c)/fxderiva(c)
        tramo = abs(xnuevo-c)
        c = xnuevo
    return(c)


# PROGRAMA #######################
import matplotlib.pyplot as plt

funcionx = lambda p: 4*p**5 - 15*p**4 + 20*p**3 - 10*p**2 + 0.6
fxderiva = lambda p: 20*p**4 - 60*p**3 + 60*p**2 - 20*p

# INGRESO
c = 0.2
tolera = 0.0000001

# PROCEDIMIENTO
raiz = newtonraphson(funcionx, fxderiva, c, tolera)

# SALIDA
print('raiz en: ', raiz)

el resultado es:

raiz en:  0.3649852264049102
>>> funcionx(0.3649852264049102)
1.4099832412739488e-14
>>>