Los conceptos de arreglos como vectores y matrices son suficientes para manejar archivos.wav. con la librería Scipy-Python.
1. Leer o Abrir archivo.wav de audio
Para procesar un archivo de audio en formato .wav, la instrucción waves.read(archivo) usa el archivo con ‘nombre.wav’ y obtiene dos variables que representan:
– muestreo: frecuencia de muestreo del sonido en PCM y
– sonido: que es un arreglo con las muestras del sonido.
El archivo de audio debe encontrarse en el mismo directorio que el archivo.py de instrucciones, por ejemplo, dado el archivo ‘Alarm01.wav’ , se puede procesar con las instrucciones mostradas:
Alarm01.wav
# Abrir un archivo de audio .wav
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
# INGRESO
archivo = 'Alarm01.wav'
muestreo, sonido = waves.read(archivo)
con lo que se obtiene:
>>> muestreo
22050
>>> sonido
array([[0, 0],
[0, 0],
[0, 0],
...,
[0, 0],
[0, 0],
[0, 0]], dtype=int16)
>>> np.shape(sonido)
(122868, 2)
En el ejemplo, la frecuencia de muestreo es de 22050 Hz. El sonido es estéreo al tener dos columnas que corresponden a los canales izquierdo y derecho.
Para usar un solo canal, se copian los datos a un nuevo arreglo. Para separar el canal izquierdo por ejemplo, se usan las instrucciones:
>>> izquierdo=sonido[:,0].copy()
>>> izquierdo
array([0, 0, 0, ..., 0, 0, 0], dtype=int16
Con lo que se tienen los datos listos para ser procesados.
1.1 Otro ejemplo de archivo.wav de audio
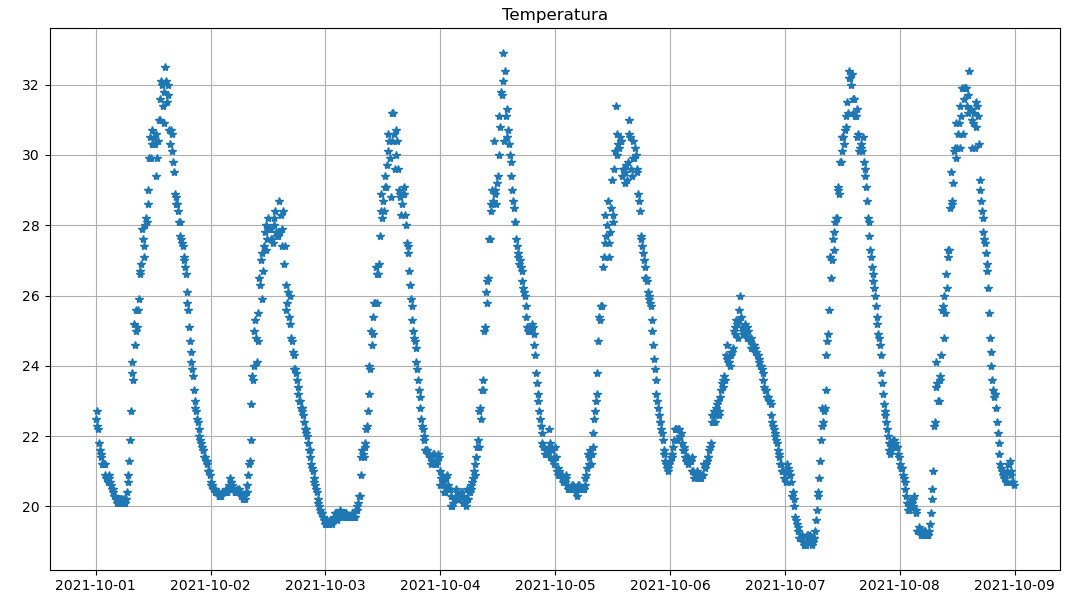
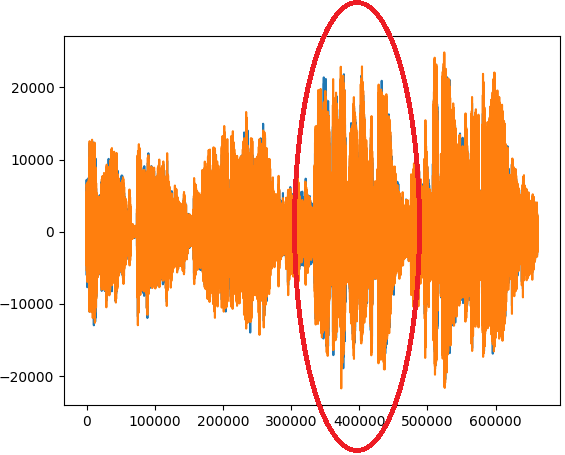
Con los datos se pueden graficar las ondas de sonido como la mostrada en la imagen.
muestra_Invernal01.wav
El formato .wav es el más simple de manejar pues contiene directamente los datos de las muestras de sonido similar a la mostrada en la figura.
El primer parámetro a obtener es la frecuencia de muestreo en Hz, o cuántas muestras por segundo se realizan, y luego los datos del sonido.
# Abrir un archivo de audio .wav
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
# INGRESO
# archivo = input('archivo de sonido:' )
archivo = 'muestra_Invernal01.wav'
muestreo, sonido = waves.read(archivo)
# PROCEDIMIENTO
tamano=np.shape(sonido)
canales=len(tamano)
tipo = 'estéreo'
if (canales<2):
tipo = 'monofónico'
duracion = len(sonido) /muestreo
# SALIDA
print('muestreo (Hz) : ',muestreo)
print('canales: ' + str(canales) + ' tipo ' + tipo )
print('duración (s): ',duracion)
print('tamaño de matriz: ', tamano)
print(sonido)
plt.plot(sonido)
plt.show()
Con lo que obtiene la gráfica mostrada al inicio y los siguientes resultados:
muestreo (Hz) : 44100
canales: 2 tipo estéreo
duración (s): 15.0
tamaño de matriz: (661500, 2)
[[-4355 -4561]
[-4353 -4572]
[-4347 -4578]
...,
[ 120 1008]
[ 124 993]
[ 100 935]]
Referencias:
https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.io.wavfile.read.html
1.2 Librerías para tratamiento de audio
la librería de funciones scipy (scientific python), dispone de funciones para el tratamiento de señales, estadísticas, audio, entre otras.
El orden de las instrucciones es el que aparece en los post del blog.
instrucciones
| import scipy.io.wavfile as waves |
librerias de audio en formato wav para lectura y escritura de archivos. |
| muestreo, sonido = waves.read(archivo) |
lectura de datos de un archivo de audio en formato wav. Se obtiene la frecuencia de muestreo y los datos en sonido |
| import scipy.integrate as integrate |
importar metodos de integración de scipy |
| integrate.simps(valrores, ejex) |
integral de muestras de señal usando el método de Simpson. |
| . |
. |
| . |
. |
2. Extraer una Porción del audio y guardar archivo.wav
Para extraer una porción de un archivo de audio se requiere: abrir el archivo, seleccionar la porción de interés y guardar el resultado un archivo de salida.
archivo origen: muestra_Invernal01.wav
archivo resultado: muestra_Invernal02.wav
La porción puede ser indicada en unidades de tiempo que luego deben ser convertidas a índices de muestras para extraer la porción requerida.
El procesamiento del archivo simplificado en Python es:
# Extrae porción de un archivo de audio .wav
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
# INGRESO
# archivo = input('archivo de sonido:' )
archivo = 'muestra_Invernal01.wav'
archivosalida = 'muestra_Invernal02.wav'
# tiempo en segundos
desde = 7.5
hasta = 10.2
muestreo, sonido = waves.read(archivo)
# PROCEDIMIENTO
# indices de muestras
idesde = int(desde*muestreo)
ihasta = int(hasta*muestreo)
porcion = sonido[idesde:ihasta,:]
duracion = len(porcion)/muestreo
# SALIDA
waves.write(archivosalida, muestreo, porcion)
print('archivo creado: ', archivosalida)
2.1 Guardar un archivo de audio .wav
Luego de procesar los datos de audio, y guardar el resultado en un archivo con ‘nombre.wav’ se usa la instruccion waves.write() de la libreria scipy, que requiere:
– archivo: el nombre del archivo resultante, con extension.wav
– fsonido: la frecuencia de muestreo del sonido (entero)
– sonido: el arreglo de la señal de audio como entero de 16 bits (dtype=’int16′).
Recuerde haber realizado el llamado a las librerias numpy y scipy que se presentan como referencia en el script.
# PROCEDIMIENTO
# Arreglos para datos con k muestras
sonidofinal = np.zeros(k, dtype='int16')
# SALIDA
archivo = 'audiofinal.wav'
waves.write(archivo, int(fsonido),sonidofinal)
El archivo de audio resultante se escucharà usando un programa como «windows media player»
Notas:
Se puede añadir al nombre la ruta de ubicación del archivo en el disco duro. Ejemplo para windows: ‘C:\Users\mis documentos\archivo.wav‘
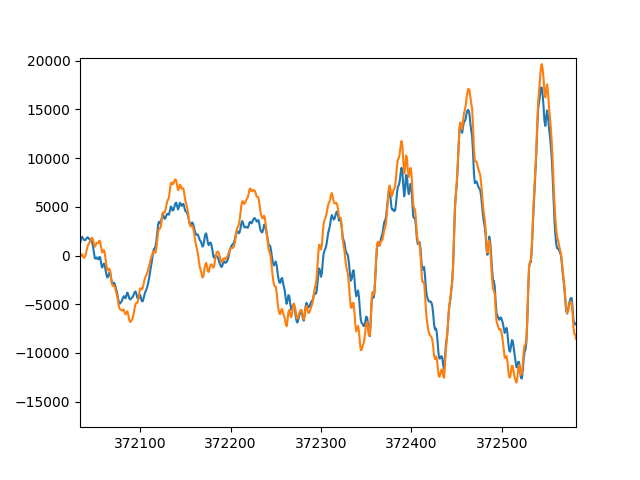
3. Gráfica de un canal de audio
Para mostrar en un gráfico un canal de audio se usa la libreria matplotlib. Para muestra, usando los datos del ejemplo anterior:
izquierdo = sonido[:,0].copy()
# SALIDA grafica
plt.plot(izquierdo)
plt.show()
con lo que se obtiene la siguiente gráfica:
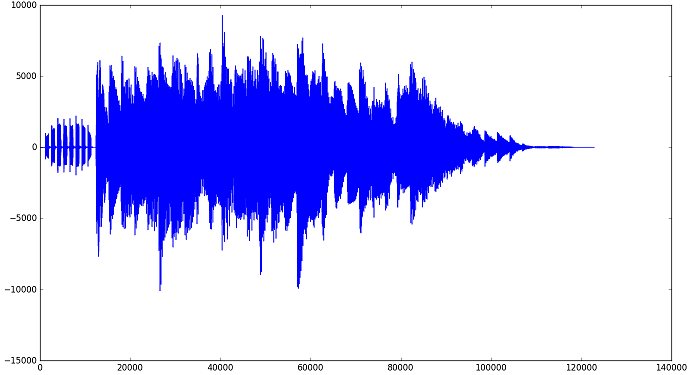
Con lo que se puede revisar la forma de la señal de audio
Ejercicio
Si el archivo de origen es estéreo, extraer un solo canal y convertirlo a monofónico.
El manejo de archivo de audio en formato wav permite analizar varios conceptos como , en los cursos de Señales y Sistemas y Procesos estocásticos:
Modulación Delta Sigma
Señales de energía y potencia
Señales Analógicas y Digitales
Correlación(señal01,señal02)
Morse – Generador de Tonos
Referencia: https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.io.wavfile.write.html