Ejercicio: 1Eva_IT2016_T3_MN Tasa interés anual
Propuesta de Solución empieza con el planteamiento del problema, luego se desarrolla con el método de Bisección y método del Punto Fijo solo con el objetivo de comparar resultados.
Planteamiento del problema
La fórmula del enunciado para el problema es:
A = P \frac{i(1+i)^{n}}{(1+i)^{n} -1}
que con los datos dados se convierte a:
5800 = 35000 \frac{i(1+i)^8}{(1+i)^8 -1}
35000 \frac{i(1+i)^8}{(1+i)^8 -1}-5800 =0
que es la forma de f(x) = 0
f(i)=35000 \frac{i(1+i)^8}{(1+i)^8 -1}-5800
Intervalo de búsqueda
Como el problema plantea la búsqueda de una tasa de interés, consideramos que:
- Las tasas de interés no son negativas. ⌉(i<0)
- Las tasas de interés no son cero en las instituciones bancarias (i≠0)
- Las tasas muy grandes 1 = 100/100 = 100% tampoco tienen mucho sentido
permite acotar la búsqueda a un intervalo (0,1].
Sin embargo tasas demasiado altas tampoco se consideran en el problema pues el asunto es regulado (superintendencia de bancos), por lo que se podría intentar entre un 1% = 0.01l y la mitad del intervalo 50%= 0.5 quedando
[0.01,0.5]
Tolerancia
si la tolerancia es de tan solo menor a un orden de magnitud que el valor buscado, se tiene que las tasas de interés se representan por dos dígitos después del punto decimal, por lo que la tolerancia debe ser menor a eso.
Por ejemplo: tolerancia < 0.001 o aumentando la precisión
tolera = 0.0001
Método de la Bisección
itera = 1
a = 0.01, b = 0.5
c = \frac{a+b}{2} = \frac{0.01+0.5}{2} = 0.255
f(0.01) = 35000 \frac{0.01(1+0.01)^8}{(1+0.01)^8-1}-5800 = -1225.83
f(0.5) = 35000 \frac{0.5(1+0.5i)^8}{(1+0.5)^8-1}-5800 = 12410.54
con lo que se verifica que existe cambio de signo al evaluar f(x) en el intervalo y puede existir una raíz.
f(0.255) = 35000 \frac{0.255(1+0.255)^8}{(1+0.255)^8-1}-5800 = 4856.70
lo que muestra que f(x) tiene signos en a,c,b de (-) (+) (+), seleccionamos el intervalo izquierdo para continuar la búsqueda [0.01, 0.255]
El tramo permite estimar el error, reduce el intervalo a:
tramo = b-a = 0.255-0.01 = 0.245
valor que todavía es más grande que la tolerancia de 10-4, por lo que hay que continuar las iteraciones.
itera = 2
a = 0.01, b = 0.255
c = \frac{0.01+0.255}{2} = 0.1325
f(0.01) = -1225.83
f(0.255) = 4856.70
f(0.1325 ) = 35000 \frac{0.1325(1+0.1325)^8}{(1+0.1325)^8-1}-5800 = 1556.06
lo que muestra que f(x) tiene signos en a,c,b de (-) (+) (+), seleccionamos el intervalo izquierdo para continuar la búsqueda [0.01, 0.1325]
El tramo permite estimar el error, reduce el intervalo a:
tramo = b-a = 0.1325-0.01 = 0.1225
valor que todavía es más grande que la tolerancia de 10-4, por lo que hay que continuar las iteraciones.
itera = 3
a = 0.01, b = 0.1325
c = \frac{0.01+0.1225}{2} = 0.071
f(0.01) = -1225.83
f(0.1325) = 1556.06
f(0.071 ) = 35000 \frac{0.071(1+0.071)^8}{(1+0.071)^8-1}-5800 = 89.79
lo que muestra que f(x) tiene signos en a,c,b de (-) (+) (+), seleccionamos el intervalo izquierdo para continuar la búsqueda [0.01, 0.071]
El tramo permite estimar el error, reduce el intervalo a:
tramo = b-a = 0.071-0.01 = 0.061
valor que todavía es más grande que la tolerancia de 10-4, por lo que hay que continuar las iteraciones.
Para una evaluación del tema en forma escrita es suficiente para mostrar el objetivo de aprendizaje, el valor final se lo encuentra usando el algoritmo.
raiz en: 0.06724243164062502
error en tramo: 5.981445312500111e-05
iteraciones: 13
>>>
Algoritmo en Python
# 1Eva_IT2016_T3_MN Tasa interés anual
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
fx = lambda x: 35000*(x*(1+x)**8)/((1+x)**8 -1) -5800
a = 0.01
b = 0.5
tolera = 0.0001
# PROCEDIMIENTO
cuenta = 0
np.set_printoptions(precision=3)
tramo = b-a
while not(tramo<tolera):
c = (a+b)/2
fa = fx(a)
fb = fx(b)
fc = fx(c)
cambia = np.sign(fa)*np.sign(fc)
if cambia < 0: a = a b = c if cambia > 0:
a = c
b = b
tramo = b-a
cuenta = cuenta+1
# SALIDA
print(' raiz en: ', c)
print('error en tramo: ', tramo)
print('iteraciones: ',cuenta)
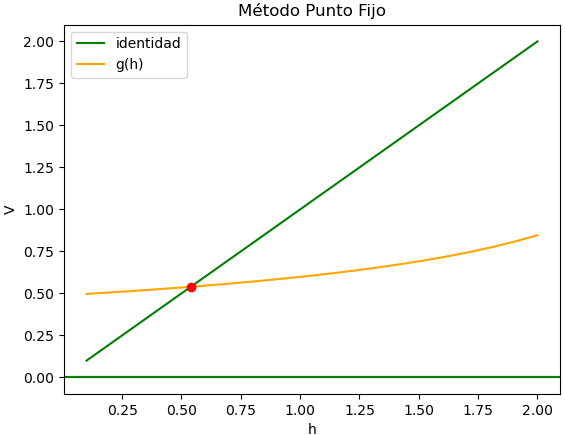
Método del Punto Fijo
El planteamiendo del punto fijo se realiza con x= g(x), por lo que se reordena la ecuación a:
35000 \frac{i(1+i)^8}{(1+i)^8 -1}-5800 =0
35000 \frac{i(1+i)^8}{(1+i)^8 -1}=5800
\frac{i(1+i)^8}{(1+i)^8 -1}=\frac{5800}{35000}
i=\frac{58}{350} \frac{(1+i)^8 -1} {i(1+i)^8}
con lo que g(x) es:
g(i)=\frac{58}{350} \frac{(1+i)^8 -1} {(1+i)^8}
valor inicial de búsqueda
Para el punto inicial i0 se puede usar uno de los extremos del intervalo propuesto en la sección de planteamiento. Para reducir aun más la búsqueda se pude seleccionar el punto intermedio
i0 = 0.255
Itera = 1
i0 = 0.255
g(0.255i)=\frac{58}{350} \frac{(1+0.255)^8 -1} {(1+0.255)^8} = 0.1387
el error se estrima como el tramo recorrido entre el valor nuevo y el valor inicial
tramo = | nuevo-antes| = |0.1387 - 0.255| = 0.1163
como el tramo o error es aún mayor que el valor de tolera, se continúa con la siguiente iteración.
Itera = 2
i1 = g(i0 ) = 0.1387
g(0.1387)=\frac{58}{350} \frac{(1+0.1387)^8 -1} {(1+0.1387)^8} = 0.1071
el error se estrima como el tramo recorrido entre el valor nuevo y el valor inicial
tramo = | nuevo-antes| = |0.1071 - 0.1387| = 0,0316
como el tramo o error es aún mayor que el valor de tolera, se continúa con la siguiente iteración.
Itera = 3
i2 = g(i1 ) = 0.1071
g(0.1071)=\frac{58}{350} \frac{(1+0.1071)^8 -1} {(1+0.1071)^8} = 0.0922
el error se estrima como el tramo recorrido entre el valor nuevo y el valor inicial
tramo = | nuevo-antes| = |0.0922 - 0.1071| = 0,0149
como el tramo o error es aún mayor que el valor de tolera, se continúa con la siguiente iteración.
Observación: Como el error disminuye entre cada iteración, se considera que el método converge, si se realizan suficientes iteraciones se cumplierá con el valor de tolerancia y se habrá llegado a la precisión requerida.
Usando el algoritmo se tiene:
iteraciones: 17
raiz en: 0.06754389199556779
>>>
Algoritmo en Python
# Algoritmo de Punto Fijo
# x0 valor inicial de búsqueda
# error = tolera
import numpy as np
def puntofijo(gx,antes,tolera, iteramax=50):
itera = 1 # iteración
nuevo = gx(antes)
tramo = abs(nuevo-antes)
while(tramo>=tolera and itera<=iteramax ):
antes = nuevo
nuevo = gx(antes)
tramo = abs(nuevo-antes)
itera = itera+1
respuesta = nuevo
# Validar respuesta
if (itera>=iteramax ):
respuesta = np.nan
print('iteraciones:',itera)
return(respuesta)
# PROGRAMA ---------
# INGRESO
gx = lambda i: (58/350)*((1+i)**8-1)/((1+i)**8)
a = 0 # intervalo
b = 0.5
x0 = 0.255
tolera = 0.0001
iteramax = 50 # itera máximo
# PROCEDIMIENTO
respuesta = puntofijo(gx,0.255,tolera,iteramax)
# SALIDA
print(' raiz en:',respuesta)